Socially-conscious investing optimized through Game theory
Investment theory follows a fairly simple premise of optimizing two primary factors of any investment: risk and reward (return). Although investors debate the most accurate ways to measure these factors, which often vary depending on the investment type or category, virtually all investments can be reduced to an attempt to maximize estimated return and minimize risk undertaken and the coinciding ratio between the two. In a recently published article, philanthropist Ian McGee employs game theory to explain how investors often inaccurately measure returns, and how cooperation can lead to a more optimal outcome for everybody.
The article focuses on the recently in-focus topic known as socially-conscious investing. When investors focus solely or primarily on monetary returns of a project, which has been the traditional measure of reward, they may miss a material significant factor in the social or environmental impact of the project at hand. Economics refers to such an impact as an externality, some consequence of the business or investment that affects other parties with which it not directly involved. Popular examples of externalities include environmental pollution from factories or combustion-engine cars, because the pollution negatively impacts our population and our planet even though the pollution itself is not some primary or intended outcome of the fundamental business. Businesses, which represent investments, regularly produce negative externalities because resolving the issue would require heavy costs and hurt the firm’s profits.
Thus, investors must make a tough decision when analyzing and comparing at certain assets: should I invest in a company with proven business model that generates healthy profits yet sickens the Earth, or should I invest in a fledgling business that wants to serve the same function as the previous but incurs higher costs to eliminate the externalities? The progressive startup company imposes a higher risk because their operations incur these higher costs and they are more likely to suffer financial stress. It can and should be argued, however, that the even though the virtuous company may have worse profit margins, their potential reward must take into account the benefit to the planet and population (this can be assessed through an increase to their own return, or a decrease to the traditional firm’s return).
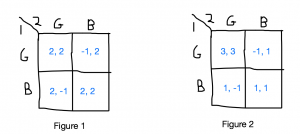
Game theory is useful in outlining this dilemma in the context of multiple investors all aiming to optimize the risk and return of their portfolios. I have attached a sketch of two payoff matrices of an investment decision, or game. The players are two independent investors and the strategies, labeled as Good (“G”) and Bad (“B), represent mutually exclusive investments in a startup company without externalities and a traditional firm with externalities, respectively. Figure 1 shows hypothetical payoffs of these investments, accounting only for monetary returns, while Figure 2 includes the impact of an externality. (The payoff numbers are representative of relative upside / return and do not have much nominal significance.)
In figure 1, note that an investment in B returns a payoff of 2, regardless of the other player’s strategy, while an investment in G returns 2 if they both invest in G and -1 if the other player chooses B. The -1 represents the added risk of investing in a environmentally friendly startup; if the firm receives insufficient funding, their high-cost business model may lead to bankruptcy and a lost investment. Conversely, the traditional firm returns 2 in both cases because they forego the costs involved with resolving the externality and already generate steady profits. If both investors choose G, I assume G receives enough funding and eventually makes similar returns to what B had made (2). In this case, the Nash Equilibrium is (B, B) because neither investor wants to risk G without a greater expected return.
In figure 2, we apply the externality to both firms: Reducing pollution provides a positive externality for G and increases its payoff to 3, while increasing pollution provides a negative externality for G and decreases it payoff to 1. Neither player here has a dominant strategy, and the result is two Nash equilibria: (G, G) and (B, B). This situation mimics a cooperation game, because even though both players receive positive returns by jointly investing in B, they total payoff is greater and they cooperate to invest in G.
Resource:
http://www.greenbiz.com/article/why-impact-investing-wins-prisoners-dilemma