The Odd Case of the Traveler’s Dilemma
In general, we have found game theory to be quite good at predicting the behavior of the participants in games. That said, even this theory has limits in the form of strange games where our predictions break down. A prime example of this is the Traveler’s Dilemma.
Here’s how the dilemma works. There is a bit of a story behind it, but that can be found in the link at the bottom of the post. The important part is:
- There are two participants
- Each chooses an amount of money between $2 and $100
- If the two amounts are the same, each participant receives that amount.
- If the two amounts are different, the lower amount a is set, and the person who gave that receives a+2 while the one who gave the higher value receives a-2.
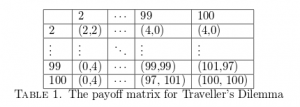
As you can see in the paper, the payoff matrix is
Now, we will try to predict what happens by looking for the Nash Equilibrium (or Equilibria).
- If participant B chooses 100, it is in participant A’s best interest to choose 99 as it has a payoff of 101 which is the maximum payoff A can receive.
- If participant B chooses 99, it is in participant A’s best interest to choose 98 as it has a payoff of 100 which is the maximum payoff A can receive.
- …
- If participant B chooses n (where n ≠ 2), it is in participant A’s best interest to choose n-1 as it has a payoff of n+1 which is the maximum payoff A can receive.
- If participant B chooses 2, it is in participant A’s best interest to choose 2 as it has a payoff of 2 which is the maximum payoff A can receive.
This argument can be gone through with A replacing B and B replacing A to see how B should react. Looking at all of these, we find that the pure Nash Equilibrium will be at (2,2). B chooses 2 → A chooses 2 → B chooses 2 → ….
But this is not, in fact, the action that most people take. Generally, both people will play 100 which will, in fact, get them much more than if they had both played 2. This tends to be the case regardless of whether or not they took time to think things through. So, what’s going on here?
In the paper found at the bottom of this post, Kudose argues that the outcome will depend on whether or not the players decide to try to play competitively or cooperatively. A model is put forth where the payoff for cooperative play is compared to the usual payoff for competitive play. Provided that the payoff of cooperative play is considerably higher, it would seem that more people would go for that option.
So, if we consider the case of the Prisoner’s Dilemma, we have a similar situation where the cooperative payoff is higher than the competitive payoff; however, it is not high enough to warrant a switch to the competitive payoff. In fact, if one were to alter the traveller’s dilemma enough, it would seem that one may revert to competitive play.
For example, what if the minimum was 75 and the amounts given (in the case of unequal amounts) were a+75 and a-75. In this case, it seems far more likely that (75, 75) would be chosen. So the approach taken in the paper seems to be on the right track.
Still, it is interesting that the model that we have been using can break down in certain games. If anything, it shows that there is still plenty of room for the field to grow.
http://math.uchicago.edu/~may/VIGRE/VIGRE2007/REUPapers/FINALAPP/Kudose%28out%29.pdf