Network Structures of Terrorist Cells
http://insna.org/PDF/Connections/v24/2001_I-3-7.pdf
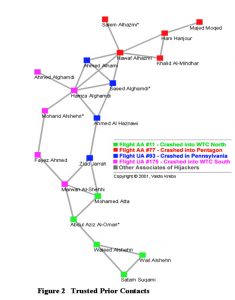
The link above links to a paper by Valdis Krebs, a researcher on organizational network analysis, discussing the many network properties of the covert networks of the terrorists of the September 11 attacks. The paper discusses the structure of the networks, taking information and data found in subsequent news articles about the attacks, carefully adding information of nodes representing people involved in the bombings, and connections (edges) between them when it is confirmed that they had met and known each other previously. The researcher then discovered that each group (groups split up by who hijacked which plane) had ties to each other, while each group was relatively separate, only having a few connections to members of the other groups. Even more surprising, he found that two of the groups had no connections to each other, connected only by the other two groups.
The above figure shows the network that Krebs constructed from the information he found. This paper has many connections to the discussion of social networks in this class, and when comparing it to some of the social networks that were analyzed in class, it is apparent that this network structure is quite similar in many ways, yet quite different. Like many social networks, we have here a relatively densely connected network of people who know each other, with weak ties out of the group, similar to groups of friends in social networks, and in this way it has many similarities to groups of friends on college campuses. However, within the group, although almost all of the edges are strong ties like a group of friends, there are very few edges in the graph, corresponding to many people not knowing each other. In comparing to friends networks, it can be more seen as a supergroup of around 2 or more smaller groups, and the more groups the supergroup is divided into, the more they resemble the stereotypical graph of social networks.
Krebs even comments on this, giving a mathematical description of these sparse connections, using the concept of mean path length between each pair of people in the graph. He writes, for a network of less than 20 nodes, there is a very long mean path length of 4.75. This means, on average, it takes a path of 4.75 edges to connect two individuals in the network. This indicates two things about the graph — first, compared to a normal social network as discussed in class, each person on average represents somewhere between a friend of a friend of a friend of a friend, or a friend of a friend of a friend of a friend of a friend. In essence, the graph is so disconnected that the speed of the travel of information is greatly hindered. Secondly, because of the structure of the graph, at least 5 of the 19 members are bridges, meaning the network would split into 2 or more pieces if they are removed. In addition, many of the other members are local bridges, and removing them would make the network even more spread out and disconnected.
While all of this would indicate that the network is relatively prone to breaking into pieces, it also means that when investigating such a graph, it would also take more time and data to connect all the members of the network. For example, in the above graph, to connect bottommost person with the topmost person, 9 separate pieces of information would be needed, each subsequent piece of information connecting one more person to the graph. Krebs mentions several methods in which members of such a group could be identified, and be shown to associate with each other. Governments could use transaction records from credit cards and bank accounts, phone, email and instant messaging records, or any other records such as real estate, courts, and car registration. As discussed in class, while such records do not indicate exactly that these people have strong (or weak) ties between each other, it shows they have had some sort of contact between each other gives a hint that they could be connected.
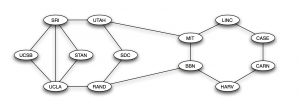
One final interesting aspect to observe about the graph is the structure of the network. Comparing it to many of the graphs seen in class, what strikes me about it is the remarkable similarity between this graph and the graph of the internet, from December of 1970.
The network of the internet was constructed to specifically have many cycles, so that if one of the edges is broken, the network still functions and information can still pass to others. Similarly, the graph of the 9/11 terrorist network has cycles (but not as many as a social network as for a single edge to be completely redundant), making the conveying of information possible even if some edges are broken. This makes the network very resilient to attack, exactly as how the internet was constructed.
One interesting question to ask is, was this network structure a coincidence of simply how the connections formed between the members, or was it deliberately set up this way? They could have set it up in a specific way, similar to a cold-war era spy ring, or it could have happened naturally. If one member gets disconnected from the group by the breaking of one edge, there is no way for that member to rejoin the network without recreating that edge. However, if one person is connected by 2 edges to two other members, if one edge breaks, whether by simply losing contact or otherwise, he is still connected and can easily remake that connection, staying in the network. The continual actions of edges naturally breaking would eventually form a network of a structure similar to that of the 1970’s era internet.