Game Theory and the Shortcomings of Modeling exhibited by Nash Equilibrium
The conflict in the Middle East is one that has spanned many decades and does not appear to have an end any time in the near future. Attempts have been made at peace, but in general, most transgressions by one side are met with an equal or greater violent reaction from the other side rather than turning to diplomacy. In an article from affairstoday.co.uk, the editor attempts to model the conflict between Israel and Egypt in the wake of the Arab Spring using game theory. This model includes the US as a third party mediator (which would likely be the case), giving a score of 1 for accepting a deal, 0 for status-quo, and -1 for refusing the deal.
It is clear from this model that Nash Equilibrium exists at Acceptance-Acceptance, as all players will receive a score of 1. Thus, accepting is a dominant strategy for all players involved. However, there are many more factors to consider such as historical opinions, differences in culture, differences in government structure, economic factors, borders, and a whole array of other problems. However, the introduction of rivalry theory and quantifying historical decisions can better explain how history and strained relations can provide a better model of this game.
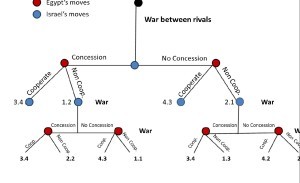
The changes that will be made to this model are based around two concepts. The first is the rival equilibrium, which suggests that in a game where both parties are enemies or rivals, they will not necessarily choose Nash equilibrium when it presents itself. In fact, it is far more likely that both players will choose an outcome that is most detrimental to the other party. This rival equilibrium exists if both parties always choose to refuse, as refusing the deal presents the fewest opportunities for gains by the rival party. The other concept is the concept of historical rivalries, and decision-making based on a previous decision. This can be modeled as a network, where each node represents a conflict and each edge connects the conflict to the resulting decision.
Once again, it is perplexing that either side would choose a Non-cooperative decision, as it almost always will lead to another war if you choose otherwise. However, in a long running game such as this a single decision could impact years of diplomacy, and brashly making a decision to cooperate could ultimately lead to a lesser payoff in the future, or worse in the case of rivalries, a higher payoff for your rival. In conclusion, it is evident that a perfect model is impossible when human emotions and ideals are taken into account. However, if the right factors are included then the model can more accurately depict these emotions by quantifying them using historical evidence and by having an understanding of how these emotions impact the decision making process of the players involved.
http://affairstoday.co.uk/what-if-game-theory-was-the-solution-to-the-middle-east-conflict/