Conditional Probability and the Upcoming Election
http://fivethirtyeight.com/features/if-trump-wins-heres-how-the-map-might-look/
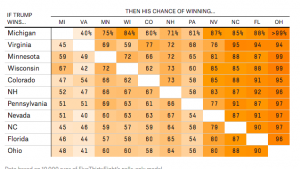
As Election Day creeps up in the next couple of weeks, it is compelling to look at the statistics and probability of each candidate voting– whether it is by demographic, location, preferences, the data on the election is exciting to follow at this time of year. Amid the almost daily polls of Hillary Clinton’s current lead on her opponent Donald Trump, Walt Hickey looked into the probability of Trump winning specific states on FiveThirtyEight. Specifically, on the conditional probability of how swing states vote based on the stance of a previous swing state.
To follow a similar method from class we will let OH = the event that Trump wins the swing state Ohio and let AZ = the event that Trump wins the swing state Florida. Then we would solve for the conditional probability: Pr(OH|AZ). From his article, Hickey included a matrix of the conditional probability that Trump will succeed in each condition. Not only is this an example of conditional probability, but this is similar to the idea of an information cascade. The varying probability that of a state being affected by the previous state’s vote is an example of how people are heavily influenced by the decisions of those who came before them.