Why you should burn the bridge behind you
In our study of network structure as it relates to bargaining power, we have found that outside options generally make an actor in a game more powerful, as these options tend to compete with one another and offer the actor choices. This tends to be true in simultaneous-move games where back and forth negotiation is allowed beforehand. In other situations, however, there exists an interesting phenomenon where having outside options can actually harm a player – let’s look at a simple game.
[Screenshot from source]
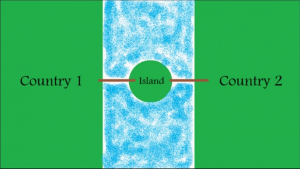
Above is a map of 2 countries separated by a river with an uninhabited island sitting in the middle of the river. Two bridges connect the two countries to the island (one from each country to the island), and these bridges are the only path from either country to the island and thus the other country. These countries would like to control the island; it is worth something. This is the situation in which we set up a game.
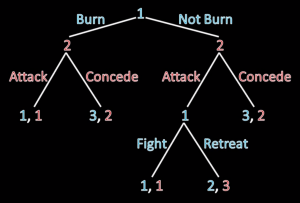
Country 1 decides to invade the island for control of it. They have two choices: they can either burn the bridge between Country 1 and the island, cutting themselves off from their homeland and eliminating their ability to retreat, or leaving the bridge as is. In this game, Country 2 then gets to decide whether it wants to attack Country 1’s troops for control of the island or if it wants to concede the island. The game ends in a battle or a concession by Country 2, unless Country 1 chooses not to burn the bridge down and Country 2 chooses to attack: in that case, Country 1 then chooses either to fight Country 2 for the island or to retreat back to its own territory.
We will now look through the payoffs of this game. Importantly, the country is not worth a lot, so if a battle does break out, the losses will strongly outweigh the benefit that the island would have provided, and we assign both fighting countries a payoff of 0 (zero); it does not matter who wins this battle, they both suffer. If no fight breaks out, one country must necessarily concede (either Country 2 cedes the l and to Country 1 or Country 1 retreats once Country 2 meets their challenge): the country that concedes receives a payoff of 2 (they did not get the island, but they did not lose anything to war) and the country that wins the island receives a payoff of 3. The payoffs and decision points are shown below.
[Screenshot from source]
We now analyze the equilibrium of the game starting from the end; intelligent players (which we assume these actors to be) would know what their opponent would do in response to their actions. If Country 1 does not burn the bridge and Country 2 attacks, Country 1 will retreat, seeing as retreating and avoiding damages puts him in a better position than engaging in a war. We then know that if Country 1 chooses not to burn the bridge, Country 2 will definitely attack. Assuming Country 2 made the same conclusions about Country 1’s likely response, Country 2 will attack because she knows Country 1 will retreat rather than fight, earning her the island and a payoff of 3, whereas conceding earns her a payoff of 2. This means that if Country 1 does not burn his bridge once he crosses it to the island, he will end up retreating and ceding the island to Country 2.
Now, if Country 1 does burn his bridge after he crosses it, Country 1 no longer has the option to retreat. Because Country 1 cannot retreat, Country 2 can be sure that if she attacks, they will both suffer loses in a war and receive a payoff of 1; there is no bluff to call. Instead, Country 2 is better off conceding in this situation, and Country 1 receives a payoff of 3, higher than the payoff of 2 he would have received had he not burned the bridge.
This is counterintuitive considering our perspective on power in a network based on structure: it seems logical that additional options – such as the option to retreat – would make a player more powerful, but in this case that is not true. Country 1’s outside option (retreating) actually made him weaker because he couldn’t credibly threaten Country 2 with war, e.g. Country 2 knew that if she attacked Country 1 would be best off retreating. By eliminating one of his own options, Country 1 committed to staying on the island. This changed Country 2’s best response, and thus changed the outcome of the game in Country 1’s favor.
This sort of commitment problem arises frequently in war, business, and other networks-based interactions. In a logical system with no trust involved, sometimes the elimination of an option adds credibility to a threat, a threat or claim which other actors would have otherwise ignored or distrusted. Imagine a prisoners’ dilemma where one prisoner isn’t given the option to rat out the other prisoner – it leads to the socially optimal equilibrium, a better outcome than before despite fewer options. Sometimes it is best to burn your bridges if it means adding necessary credibility to an otherwise flimsy claim.
Source:
- Game Theory 101 MOOC (#22): Tying Hands (Burning Bridge), https://www.youtube.com/watch?v=bxIrKkGRpBY, Published September 18 2012.