Nash Equilibrium in Hospital Overcrowding
Today, one of the biggest challenges hospitals around the country face is overcrowding. As the nation’s population increases, as well as the percentage of insured constituents, hospital beds are filling faster than ever. In response, hospitals all over the country are using dwindling finances to expand in order to absorb these new clients. However, observing this issue in Game-Theory models shows that overcrowding is the equilibrium state of hospitals in our current health care system, and expanding will only result in the same problem on a larger scale.
Let’s first replicate the problem using two patients. Both patients would like to receive the best care they possibly can, and we assume that less crowded hospital spaces results in better care. Satisfaction with the care they received is based on a scale of 1 to 10 (assuming 1o = best). The two patients are choosing between going to their Primary Care Provider’s office or go directly to the ER. If both patients go to their PCP, it gets crowded, and if both patients go to the ER, that gets crowded as well. So there results in four possible scenarios: they both go the ER (1,1), patient one goes to the ER and patient two goes to the PCP (8,8), patient one goes to the PCP and patient two goes to the ER (8,8), and both patients go to their PCP (1,1). In this situation, there is no common strategy to either go to the PCP or to go to the ER to achieve a Nash Equilibrium. Whenever one patient goes to one place, it would be better for the other patient to go to the other place.
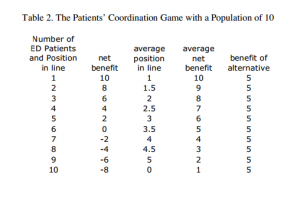
However, this model is too simple – obviously there exists more than two patients that go to the same hospital/PCP combination. Let’s look at the problem using 10 people. Below is a table of sample data from the article:
Looking at this data alone, we can first see that if less than six patients choose to go to the ER, then the ER would be the best choice (instead of going to the PCP), since you would get a non-negative net benefit from going. If more than 6 go, then the individual’s best response would be to go to the PCP instead. Therefore, in order for a Nash Equilibrium to occur, six of the individuals must choose the ER while the other four choose the PCP.
Looking at this, we can conclude that expanding the hospital won’t solve the over-crowding issue. If we increase the size of the hospital so it can accomodate more patients, then more people would make the choice to go to the ER up to the point that the expected benefit of going to the ER is equal to the expected benefit of going to their PCP.
This study just proves that Nash Equilibrium is not just effective for solving economic or mathematical problems, but rather that many problems in the real world can be manipulated and shaped into game-theory models and can be solved!