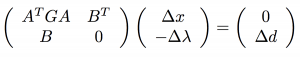The negation of the Braess paradox as demand increases
In 2010, Anna Nagurney, a professor at the University of Massachusetts Amherst, published a research paper under the heading, “The negation of the Braess paradox as demand increases: The wisdom of crowds in transportation networks.” Her goal, as the title suggests, was to prove that as demand increases, the Braess Paradox disappears. As was discussed in class, the Braess Paradox occurs when the addition of a new road in a network actually increases the travel time for each individual driver.
The hypothesis of her paper is that “in congested networks, the Braess Paradox may ‘disappear’ under higher demands.” She proceeds to prove this by creating a formula that will provide the increase in demand necessary to guarantee that the new additional road is not used and, thus, the new road does not increase travel time.
She begins by outlining that congested networks depend on the behavior of the users and that there are typically two types of behavior. One is user-optimizing behavior which is similar to what we discussed in class in that each traveler chooses a route that would optimize their travel time; the second is system-optimizing behavior in which a central controller would decide who took what route. She notes that the Braess Paradox only occurs under the user-optimized behavior when an additional route slows down the travel time for every driver. She proceeds to derive a formula that will give the amount of increase needed for any network that experiences the Braess Paradox. After a lot of complicated math derivation, she arrives at the following linear system:
This system relates the change in path flows to the change in demand. She then applies this system to a network in which the Braess Paradox occurs and shows that, after a certain level of demand (i.e. more cars on the road), people will no longer take the new route and the flow through that route will be zero.
This relates to a variety of things we have been learning in class and we can even apply this principle to an example given in class to show that it works. While I am unable to apply the math they used in the research paper, as it is too advanced, I am able to apply the idea to show that it works. The following example was taken from the lecture on Traffic in Networks.
As was shown in class, if we have 200 drivers that want to travel from node A to node B, we know at Nash Equilibrium 100 drivers choose the route ACB and 100 drivers choose the route ADB. This results in a travel time of 35 minutes. Just like in class, we will now add a new route so the network now appears as follows:
Again, we know from class that all drivers will take route ADCB and will have a travel time of 40 minutes. This is an example of the Braess Paradox as the addition of a new route has increased travel time. I can now apply Professor Nagurney’s hypothesis by increasing the demand so that there is now 1000 drivers. We now find that, at the Nash equilibrium, 500 drivers take ACB and 500 drivers take ADB. Thus, the new route with a time of zero is not used at all as no driver has an incentive to take that route because it will increase their travel time from 75 minutes to 100.1 minutes. Thus, we have eliminated Braess’s Paradox as adding the road from D to C does not change the travel time as no driver takes it. Equally interesting, if we decrease the demand, say there were only 20 drivers, then the addition of a new route would decrease the travel time from 26 minutes to only 4 minutes. Professor Nagurney’s research has a lot of impactful implications for designing roads and deciding when new routes should be added. It is very important to think about how many drivers will be on the roads as adding additional roads could either speed up travel time, slow travel time or perhaps, even worse, cause new roads to not even be used.
Source: https://supernet.isenberg.umass.edu/articles/NegationoftheBraessParadox.pdf