Threshold and coordination models in the varying desirability of the Facebook internship
https://www.nytimes.com/2018/11/15/technology/jobs-facebook-computer-science-students.html
nytimes.com/2018/11/15/technology/jobs-facebook-computer-science-students.html
With its hefty paychecks and renowned status, the Facebook internship is one of the most desired internships for software engineering students worldwide. But this may no longer be true in the future. Facebook has been the center of several political and privacy controversies for quite some time now, causing some students to no longer desire a job or internship at Facebook. As one student states, “Before it was this glorious, magical thing to work there. Now it’s like, just because it does what you want doesn’t mean it’s doing good.” There is an increasingly negative social view of Facebook, and it is definitely understandable why some students are rejecting Facebook despite its great perks such as free food and good pay. It is very interesting to see this shift in perspective towards Facebook from these students’ point of view, since I can relate as a CS major. It is also interesting to analyze this social phenomena as a threshold and coordination model.
We can model this shift in perspective as a coordination model. Let the network consist of people as nodes, with edges between people that directly know each other. Next, for simplicites sake we assume everyone in the network gets an internship offer from Facebook. Thus we will model strategy A as accepting the Facebook internship, and strategy B as rejecting the hypothetical offer. For simplicities sake, let the initial state be such that everyone is choosing strategy A, i.e. everyone wants to accept the Facebook internship. For the coordination payoff matrix, I will provide two payoff matrices. First consider this:
Let this be the payoff matrix for when the controversies were just starting. The reasoning for these values is the following. Assume everyone has a Facebook internship offer, as well as other internships from less prestigious companies with less perks. Also assume that everyone has some degree of a negative view towards Facebook due to the recent scandals. Despite this, the internship at Facebook has great perks and gives lots of bragging rights, so strategy A gives you a very high payoff of 100 per neighbor that also accepts the internship. If you reject the internship, you don’t get the great perks and bragging rights, but you can still accept the other internship so you get a lower payoff of 50 per neighbor that also rejects the internship. If you accept the internship while your neighbors in the network reject the internship, you still enjoy the great perks of Facebook but you face some social judgment so you have a slightly lower payoff of 80. It is clear to see a dominant strategy of accepting the internship with this payoff matrix; no matter what your neighbor does, you always get a higher payoff by accepting the internship. Thus it does not matter even if all your neighbors reject the Facebook internship; you should always accept the internship. The math works out as well; consider a node with n neighbors, where a fraction p of those neighbors choose to accept the internship. Then the payoff of also accepting the internship is n*p*100 + n*(1-p)*80 = 80n-20np. The payoff of rejecting the internship is n*p*50 + n*(1-p)*50 = 50n. A person accepts the internship if the payoff of accepting is greater than or equal to the payoff of rejecting, i.e. if 80n-20np >= 50n. solving this inequality gives us that a person accepts the internship if the fraction of neighbors accepting the internship is less than or equal to 1.5. The interpretation of this proportion being greater than 1 is that you ALWAYS accept the internship. And this is mostly what the perspective was initially for software engineer students. If you get an internship from Facebook, you’re definitely taking it.
But what is happening now that is causing students to begin rejecting the internships? Consider the following quote from the article: “Ms. Brown said she thought that could change soon, though, as the social stigma of working for Facebook began outweighing the financial benefits.” The answer is that the public view of Facebook is becoming more negative. Thus the payoff for accepting the internship when your friend reject it is going down. Consider the following matrix:
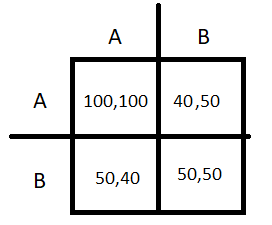
What has changed is that your payoff for accepting the internship when your neighbor rejects it has decreased from 80 to 40. Now, the total payoff of accepting the internship when you have p fraction of n neighbors that accept the internship is n*p*100+n*(1-p)*40 = 60np+40n. The payoff of rejecting is then n*p*50 + n*(1-p)*50= 50n. Thus a person will accept the internship when the payoff for accepting the internship is greater than or equal to the payoff of rejecting the internship, i.e. when 60np+40n >= 50n. Solving this inequality gives us that you only accept the internship when 1/6 or more of your neighbors accept the internship. What has changed is, you do not always want to accept the internship with this payoff matrix. And following the current trend, the payoff of accepting the internship when your neighbors reject it will only keep decreasing if Facebook keeps appearing in the news in a negative light. And everytime a Facebook appears in the news again due to a controversy, there may be more initial adopters for strategy B because people may be convinced to reject Facebook internships. Thus this model explains the phenomena we are seeing where students are beginning to reject the Facebook internship.
The rapid development of the tech industry is definitely unlike any industry in history, and it is both fascinating and frightening to wonder what direction it will move towards.

