The Game Theory behind Magic: The Gathering and Shandalar
Article: https://magic.wizards.com/en/articles/archive/introduction-game-theory-2007-05-30
Previous post: https://blogs.cornell.edu/info2040/2016/09/09/game-theory-in-magic-the-gathering-2/
Collectible card games (CCGs) nowadays have started to die down, but back in the 90s they reached their heyday as THE method of entertaining oneself through games. YuGiOh, Pokemon, Bakugan and more all seem to come to mind. However, there’s one card game that pretty much rules them all.
Magic: The Gathering.
Magic, often abbreviated to MTG for short, is a game with a large, diverse card pool: players can construct decks by selecting cards from this pool in order to gain some competitive advantage. In a normal game, each player starts with roughly 20 life, and must deal damage to each other by playing spells and powering those spells with “lands.” The individual deck composition, in this case, is extremely important: understanding what decks have spells that can counter each other, along with ensuring that players draw enough lands to power their spells and enough spells to put their lands to use and analyzing the board to surmise the potential state of an opponent’s hand.
Understanding both what deck to make and how to play are both cases of game theory and best responses: what would the best response be in the given situation? However, in both cases, real life throws two wrenches into an otherwise simple game theory problem: the lack of information about the opposing deck, and the lack of information about the current game state.
On one hand, it’s impossible to know the deck which the opponent would be able to play, and this is talked about in more detail within the article. Because there’s a fairly clear understanding of the matchups between individual decks and deck types, running a Merfolk or “Pure Blue” deck may end up doing well against a Goblin (“Pure Red”) deck, but do poorly against a green deck which focuses on using Giant Growth to buff individual creatures, while a “Pure Red” deck might fair better against a Green deck because of its relative speed (while Green takes a while to get off the ground).
The article itself focuses on a specific case in which the individual decks are not well known: the MTG Draft format. Within this format, players must choose from a limited pool of semi-random cards by picking cards one at a time. Individual decks, known as “Silvers,” are considered extremely powerful within this format, but are chock-full of cards which must be put together in order to work properly. Therefore, if one player drafts Silvers while others do not, this player would have an edge, but if multiple players attempt to draft Silvers, the individual cards in the card pool would be split between them and their decks would suffer as a result. Because individual players would gain more out of drafting Silvers in each individual situation within the article, drafting Silvers becomes a dominant strategy, yet doing so reduces the total likelihood that each player would win a match based on the table mentioned: a classic case of the prisoner’s dilemma. If both players were to collude, they could attempt to raise their combined chances of winning, but doing so wouldn’t be particularly rational, as MTG is (after all) a zero-sum game, and thus drafting Silvers when the opponent is not (breaking any agreed-upon pact) is more rational.
The article then considers best responses with regards to an individual turn being played, in this case illustrating an individual turn being played, and whether it was in the player’s best interest to engage with an attack in order to win a game given items in their hand which an opponent wouldn’t know about (more specifically, a “Giant Growth” card). This idea primarily encompasses the lack of information one has when playing a game of Magic: The Gathering, and the understanding that one can get information about what the opponent’s own best response could be given the current state of the board (the number and type of mana available, the number of cards in the opponent’s hand, and the opponent’s deck type). By using this sort of gathered information, it becomes easier to create an understanding of an opponent’s most likely “best response” in a given situation.
That being said, how exactly can we model this (especially if someone like me doesn’t have the money or time to invest in getting cards and playing Magic physically) in a more realistic way? One extremely desirable option is to consider an old game by MicroProse: Shandalar, a video game where one can save a given setting in MTG by playing the card game against AI opponents. Through this game, we can have a better understanding of what an opponent’s “best response” would likely be given a move we make, and what our “best response” should be given an opponent’s move.
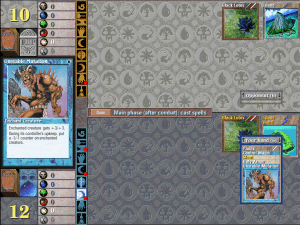
Let’s take a specific example from a current game that I’m playing. In my case, I’m playing what I would coin an “Abjuration Air Force” deck. This deck, colored “blue” (control) and “white (protection), revolves around using the “Moat” enchantment to block powerful ground forces and only enable flying creatures to attack, while building a sizeable force in the air (using Air Elemental, Ghost Ship, Serra Angel, etc.), along with other blue and white cards (Control Magic, Brainwash, Prodigal Sorcerer, etc.) to negate potential strategies the opponent can come up with and potentially buy time to ensure that I can “go wide” with a large number of creatures and attacks. However, the video game can fight back: in the example match I show, the opponent (despite being a lower-level enemy) has the ability to copy the same deck that I have, including some of my more powerful cards.
More specifically, I know that the lower-level enemy would normally not have a “Black Lotus” in their deck, but because they played it and an Island (a type of land) on the first turn, I know that the enemy probably has the same deck (and usually the same hand) as I would. This introduces an interesting strategy: because I have a “Control Magic” card, I can take control of any of the higher-powered monsters on their side of the field. However, because they have a “Control Magic” card (as they have the same hand/deck), they can do the same to me, and we both (through the Black Lotus) have enough mana to play any spells we need to play.
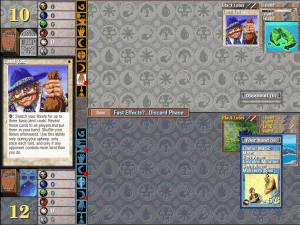
This also throws a wrench into my normal win condition. Because they have the same deck as me, playing a “Moat” wouldn’t really help me in any way: the other deck also has really strong flyers and can play “Moat” as well. The only option here is to continue to play lands and bide time, potentially playing lower-level creatures in the process to cause the AI to aggressively use Control Magic.
This goes on for a few turns:
In this case, I have more powerful cards in my hand (Serra Angel, Mahamoti Djinn, etc.) but I know that I can’t play them because the best response of the enemy would be to play “Control Magic” and take them over. The best response I would have to that would be to either play “Control Magic” again to regain control, or to wait until I can get a more powerful blocker out (and in either case, I would be taking quite a bit of damage before I can “stabilize”). Just like in economics and game theory, I need to base my strategy off of what my opponent would rationally do and analyze what the opponent is capable of, using this to (roughly) understand the value of the individual board after a move by both players. Unlike the basic game theory models we’ve used in class, it’s not easy to simply quantify the values of a board to each player: even if a player has less life than their opponent, they may still have the “upper hand” through some existing card on the field, a large number of creatures on the field, or a card in their hand that can change the playing field completely. Likewise, neither player possesses perfect information: while I know that in this case, if my deck is copied by my opponent, then my hand is most likely copied as well, I can’t necessarily know what the opponent can draw next and what the opponent can currently play: this is seen when the opponent plays “Land Tax” (a card I don’t have in my hand) by presumably drawing it after the opening hand.
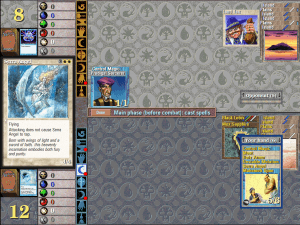
Unfortunately, I don’t have a screenshot of the next bit, but I eventually draw a “Prodigal Sorcerer,” a smaller card that can still deal 1 damage per turn. In this case, I can play it (I have enough mana to do so) and I can essentially put the opponent on a “10 Turn Timer:” if they don’t do something to counter or negate the card I currently have, I can win in 10 turns at most. Because of this pressure, I can analyze that the opponent’s only responses would be to either stall (in which case the opponent would take a lot of damage) or to attempt to play their own creature or control my creature.
Controlling my creature is exactly what they did:
While this would be the best response of the opponent, given that they now have me on a 12 turn timer (by simply using the sorcerer to deal 1 damage to me every turn), I now know that they used their Control Magic spell, so my best response would be to play a higher-level creature (Mahamoti Djinn or Serra Angel) in order to deal more damage to the opponent and win the game.
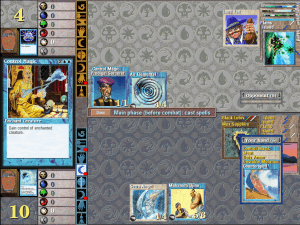
That’s exactly what I do. I start by playing my Serra Angel (a powerful creature that can deal 4 damage while flying), and eventually my Mahamoti Djinn, and even if they were able to play a flying blocker, I could simply negate it by casting “Control Magic.” The final board looked as it did below:
In this case, I had two creatures with flying out, and the opponent only had one. If I proceeded to cast Control Magic on the Air Elemental, I could then win the game by attacking with impunity, and even if the opponent’s best response was a “Counterspell,” I also possessed a “Counterspell” and could use that to block their attempt at negating my move.
Ultimately, I hope that this blog post showed the interesting applications of game theory to a well-known collectible card game! Whether it was through applying the Prisoner’s Dilemma to deck decisions as the article mentions, or by analyzing potential best responses in an opponent’s deck during a match even without complete information (as the article and video game show), Magic: The Gathering has a lot of neat applications of concepts in economics and game theory! The video game mentioned above (Magic: Shandalar) is currently abandonware: while the game itself was developed by MicroProse for the MS-DOS, it eventually was made free-to-download and free-to-use, and it’s been a great way for me to get into a card game I’ve never played as a kid!