Settlers of Catan and Game Theory
Settlers of Catan is a board game where players gather resources and make buildings. The board is an arrangement of hexagonal tiles with each one containing a resource and a number; during each turn, if the number on a tile is rolled, the player(s) who has buildings on that tile collect the resource from that tile. The goal of the game is to reach 10 points by using resources to construct buildings that are worth different amounts of points. The article describes the value of each resource during each stage of the game, for example, data collected from winning players show that wheat is the best resource to place your initial buildings on. It also talks about what resources are the best to expand to once you’ve established your initial buildings: wheat is still the best resource, however the second best resource to expand to is wood whereas the second best resource to start on is sheep. Using this information, players can develop their optimal strategy for winning the game.
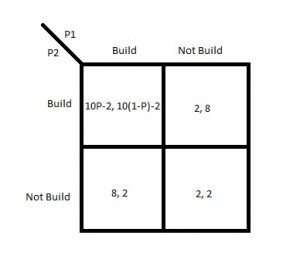
The article only talked about strategies for an individual player, but we can apply the knowledge we learned in ECON 2040 to construct a more developed scenario with two players. Consider the case where two players are competing for the same resource tile, but they must build a road (that costs 2 resources) before they can claim it. Let’s say the resource they are competing for is wheat which is very important so we will makes its value 10 resources. Player P1 goes first, then Player P2 decides what he wants to do; when it’s Player P1’s turn again, if he has accumulated enough resources to make a building (let’s say this has a probability P of happening), then he builds on the tile and claims it, if not, then Player P2 will claim it on his next turn. Using this information we can construct a table:
If both players build a road, then P1’s payoff is the probability that he can claim the tile times the value of the tile minus the cost of building the road and P2’s payoff is the same except with the probability that P1 cannot claim the tile (which is 1-P). If one person build a road and the other does not, then the one who built the road claims the tile and has a payoff equal to the value of the tile minus the cost of building the road (which is 10-2) and the player who did not build a road gets a payoff equal to the resources he would have spent building the road. If neither player builds a road, then they both gain the resources they would have used to make the road.
If the players can estimate the probability P, then they can determine an optimal strategy for this situation; let us say that the value of P is .5, then the payoffs for both players if they both build is 3. In this case the dominant strategy for both players is to build a road.
http://developingcatan.files.wordpress.com/2011/02/settlers-of-catan-analysis.pdf