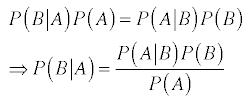Bayes’ Rule, Meadow’s Law, and Fooling Juries
In 1977, British Pediatrician Row Meadow published highly controversial work on the Münchausen syndrome by proxy, a term used to describe when a “caregiver deliberately exaggerates, fabricates, and/or induces physical, psychological, behavioral, and/or mental health problems in those who are in their care”. Following this event he often served as an expert witness on trials having to do with Sudden Infant Death Syndrome (SIDS) or “cot death” and in doing so helped spread the idea that “one sudden infant death is a tragedy, two is suspicious and three is murder, until proved otherwise“, an idea that came to be called Meadow’s Law.
People serving on juries bought into this reasoning for many years, but critics of Meadow’s Law were eventually able to upturn the theory on the grounds that Meadow’s claims were simply not based off good statistics. In particular, while testifying during the high-profile case of Sally Clark who was accused of murdering her two infant sons in 1999, Dr. Meadow claimed that the chance of her two sons dying suddenly and randomly due to SIDS was 1/73,000,000. Where did this number come from? As explained by Peter Donnelly in the TED talks video, Dr. Meadow had looked up the chance that one infant would die of SIDS in a non-smoking household (~1/8500) and squared it because there were two children. As Mr. Donnelly points out, the first fallacy with Dr. Meadow’s claims logic is that the math simply does not work like that in this scenario because the two deaths are not necessarily independent (and in fact probably were not). Furthermore, what Dr. Meadow later tried to conclude can be considered an improper application of Bayes’ Rule which we learned during class.
More specifically, according to Bayes’ Rule:
In this case, event B could be taken as the probability that Sally Clark murdered her two sons given event A that her two infant sons died. In other words, Dr. Meadow had calculated (incorrectly) the probability of event A (that the two infants died of SIDS) and then assumed that the only logical explanation for the contrary was that Sally Clark had murdered her sons. That is, he claimed that the chance the Sally Clark was innocent was a mere 1 in 73,000,000! What he should have done is compare this probability that Sally had killed her sons given the deaths of her two infant sons to the probability that her two sons had died from SIDS given the fact that they had died. That is, apply Bayes’ rule to both scenarios and compare the relative likelihoods. Yes, the chance that both children died of SIDS is very low (not quite 1/73,000,000), but still pretty low. However, we would hope that the alternative (that a mother would murder both her children) would also be very low.
Unfortunately, in this case neither lawyer doubted the validity of Dr. Meadow’s claims and the jury (understandably) found Sally Clark guilty of murdering her two sons. Furthermore, while Sally was eventually acquitted of the crime, it undoubtedly caused her to suffer an immense amount of emotional trauma and she was found dead of alcohol poisoning in 2007. In conclusion, Bayes’ Rule is clearly an extremely useful tool in statistical inference, but cases like these demonstrate that we need to be very careful with its application and the application of statistics in general.
-porcupineh
http://www.ted.com/talks/peter_donnelly_shows_how_stats_fool_juries.html
http://www.dailymail.co.uk/news/article-206417/Professor-created-Meadows-Law.html#