Braess’s Paradox in a Computerized World
http://www.cnn.com/2012/09/18/tech/innovation/ieee-2040-cars/index.html?hpt=te_r1
It’s a very bold title, “You Won’t Need a Driver’s license by 2024”. But perhaps it isn’t too farfetched. As the article says, Google has already developed a driverless car, and they have even made it street legal in Nevada. Many people (myself not included) would relish the opportunity to leave driving to a computer system and never have to worry about switching lanes or parallel parking again. But will people really switch from traditional cars to automated cars in the near future? Jeffery Miller, who is quoted at the end of the article, certainly believes so, “As more vehicular controls begin being automated, such as parallel parking and automatic braking, people will become more accepting of autonomous technologies. So by 2040, driverless vehicles will be widely accepted and possibly be the dominant vehicles on the road.” But I think it is interesting to look at this claim in the context of networks and game theory.
Let us consider an example of Braess’s paradox, in which a supposed improvement to a road system is actually detrimental to travel time. In this instance, there are 400 drivers who have to choose between two routes from city A to city B (pictured below). The travel time of edges C-B and A-D are proportional to the number of cars on them. If we assume that the drivers do not communicate and act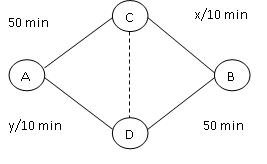 
purely on self interest we actually arrive at the optimal traffic pattern, half of the people down each route for a total travel time of 70 minutes. This is because if either A-C-B or C-D-B has more people on it than the other the road less travelled will be faster and someone will switch routes to improve their travel time. The only stable equilibrium, in which no one can act to improve their travel time is a 50/50 split. Now imagine that route E (dashed line) is built, connecting C and D with negligible travel time. If everyone acts on self interest, they will all use this new route since edges A-D and C-B are always quicker than A-C and D-B (even with 400 people on them!), resulting in a travel time of 80 minutes. Bizarrely this “improvement” actually increases the travel time for everyone. Surely automated vehicle would avoid this problem. But is this the case? If the entire 400 car fleet were automated, then the computer system would dutifully send half of the cars through A-C-B and the other half through A-D-B, ensuring the shortest travel time for all. But what if people were not forced to buy the automated cars? If we assume that the computer rigidly sticks to the 50/50 split then any individual can decrease their travel time by buying a traditional car and using the third route and we are back to the original problem. Once again, individuals acting in their own self interest will increase travel time for everyone.
Of course this is an oversimplification, and actually serves to highlight one huge advantage of automated cars. The critical part of this problem is that some of the edges travel time depends on the number of cars on them. In an automated system, this effect would be weaker or nonexistent. In this system, all of the cars would know exactly where all other cars are, how fast they are going, where they were getting off, etc. This would allow them to travel much closer together and at higher speeds since they don’t have to worry about reacting to unexpected moves by the cars around them. To model this, say that the travel time for all edges is independent of traffic, if you have an automated car. As long as this set time is shorter than what traditional cars can achieve, people will quickly adopt driverless cars.
-Jay