The Nancy Pelosi Game
As we get closer to Election Day, it is particularly interesting to analyze how the decisions of politicians and the voters may affect each other and the outcome of an election or nomination, from the perspective of game theory. Earlier this year, Jonathan Day, et. al published an article in the Journal of Game Theory examining whether or not a comment made by Nancy Pelosi played in her favor.
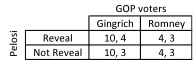
The game set up by the research team is based on Pelosi’s revealing that she had secret information against Newt Gingrich that would preclude him from winning the presidency. However, she did not reveal what that secret was, merely that she possessed such information. At the surface, it makes sense that Pelosi would save the secret for later so that Gingrich, presumably the weaker candidate compared to Mitt Romney, would have a better chance of being nominated, which would in turn give Obama a better chance of winning. But the real question is why Pelosi would reveal at all that she had information against Gingrich.
The payoffs were assigned by the group using the following scheme. The value of Obama being reelected is 10, the probability of Obama winning against Gingrich is 100%, and the probability of Obama winning against Romney is 40%. The payoff for Pelosi equals the value of Obama’s reelection multiplied by the probability of Obama winning against the Republican nominee. For the voters, the value of having Gingrich as president is 10, while the value of having Romney president is 5, since Gingrich is more conservative and is thus preferred ideologically. However, the probability of Gingrich winning against Obama is 30%, while the probability of Romney winning against Obama is 60%. If Pelosi doesn’t reveal the information, the payoffs are the probability multiplied by the value. If Pelosi reveals the information, the voters may think Gingrich has a lower chance of winning against Obama (say, 25%), but they may put more value on Gingrich (say, 16), seeing him as the “nemesis of the Democrats.” Based on these payoffs, we can see that it is actually better for Pelosi to reveal that she has secret information, since the voters’ best response would then be to nominate Gingrich over Romney, a good outcome for Pelosi.
I think this game reveals simultaneously an advantage and shortcoming of modeling such political situation as a two-person game. First, the game is a good way to simplify many, otherwise complex, variables. Considering each candidate’s chances of winning, the voters’ ideological preferences, and the voters’ thoughts after Pelosi’s comment, it is difficult to predict what Pelosi’s best strategy might have been. Reducing these variables to single-number payoffs, however, also reveals a shortcoming: it seems the validity or practicality of the model may suffer by arbitrarily assigning numbers to unquantifiable variables. Couldn’t the outcome change if the numbers were assigned differently? One way the article overcomes this is by applying statistics. For the voters’ payoffs in the case that Pelosi reveals the information, the research team looked at a range of possible values for the increased value of having Gingrich as president and the decreased probability of Gingrich winning against Obama, and showed that 78.8% of the combinations would still favor Pelosi revealing that she had secret information. This application of game theory to a subtle political situation shows how a counterintuitive decision may actually be the optimal one. Furthermore, if one politician’s decision to say something can be modeled as a two-person game to arrive at a counterintuitive result, one can imagine how game theory can be a powerful tool for analyzing the complex interactions that affect electoral politics.
— Mr. J
Source:
http://article.sapub.org/10.5923.j.jgt.20120102.01.html