Google Maps–it’s just one big graph
Anyone who has had the luxury of looking up directions on how to get somewhere on Google Maps has likely ignored or disregarded the intricacies of how such a path is calculated. The entire premise of Google Maps is using a big giant graph with nodes and edges to figure out fastest or shortest way to travel. That’s all Google Maps is–a big graph with lots of nodes and edges. However, given the large amounts of data that would be needed to analyze a large graph and keep track of all its nodes and edges, it is impressive that such a calculation can be performed by Google in such a short time.
This section from the paper by E. W. Dijkstra (http://www-m3.ma.tum.de/foswiki/pub/MN0506/WebHome/dijkstra.pdf) written in 1959 outlines the basic methodology that Google uses to make this calculation. The graph in question would look something like the following:
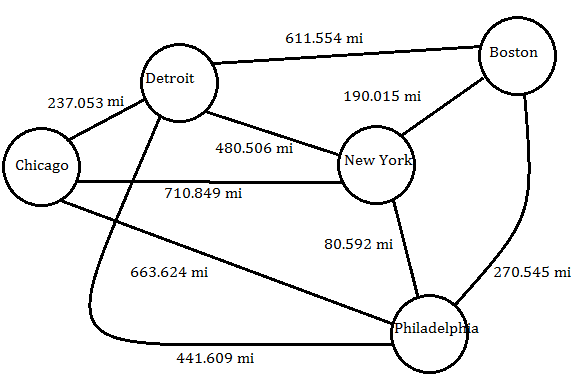
( Note: this graph is simplified and not to scale )
The above graph shows five major cities in the northern, northeastern part of the U.S. (these are the first five that came to mind). Each node is a city and each edge in the graph represents a straight flight path distance that, say, a crow would take while going from one node to another. These distances were calculated using http://www.freemaptools.com/how-far-is-it-between.htm
Realistically, this is not an ideal path since most people who use Google Maps are not crows nor can they take a straight flight-path. This is especially true since this theoretical path would go through water or terrain without roads. Since this graph shows edge permutations between every node, it is quite obvious what the “shortest distance” between two nodes would be (since the shortest distance between any two points is a straight line). However, not all major cities are directly connected in this sense. There are many roads that would be required to take to actually traverse from one node to another. In the case of Google Maps, these roads would be represented by edges on the graph. The graph used by Google Maps would include many more nodes ranging from other large cities and smaller cities to villages or even street intersections. Since Google Maps can take someone from one address to any other address (for the most part), then one can only imagine how many nodes there are in the full graph. It would take a long time to calculate the shortest path by hand–and an non-viable amount of time through the computer. However, this action is performed fairly quickly by Google Maps many times in a short period of time.
The secret is quite simple. Dijkstra’s algorithm as outlined in the paper is one of the many ways to finding such a path but other ways are also valid as outlined on the wikipedia page for path-finding,http://en.wikipedia.org/wiki/Shortest_path_problem
Google can facilitate this problem by encompassing nodes within other nodes. If someone wants to find the shortest distance between Philadelpha and Boston, it would not be viable or wise to include nodes such as Seattle in the graph during calculation. Clearly, Google Maps would take a sub-section of the entire graph and work only on that portion. What if we had a giant node called “Northeastern US” which encompassed the graph for all the cities in that region? Perhaps within that node, we can have other nodes such as one called “New York” that focuses only on a graph with nodes that fall into that category. The closer the cities are to each other (as it can visually be seen via the “zoom” feature) then the less work that would have to be done. Let’s consider this next graph:
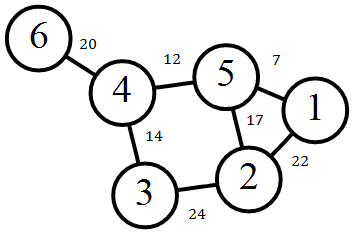
( Note: this is also not drawn to scale ). This graph came from the wikipedia page posted earlier with minor modifications.
We can take each node to be a node in Google Maps (so it could be a city, intersection, or someone’s house) and an edge to be the distance between two nodes (could be a road or a sidewalk). An edge could represent a road, sidewalk, or something similar. In this case, using a methodology such as Dijkstra’s algorithm as outlined in the second half of his paper would allow a program such as Google Maps to calculate the shortest distance. In the case of this graph, we as people can see that the shortest distance from nodes 3 and 1 is going 3 -> 4 -> 5 -> 1 and not 3 -> 2 -> 1 because the of how the values of the edges add up ( 14+12+7 < 24+22). Systematically, a computer program running Dijkstra’s algorithm would also arrive at the same conclusion in terms of shortest distance. Simply following the step-by-step instructions listed in the paper could guide you through how a computer would perform this problem.
Although this problem on larger graphs would be more difficult, Google has multiple high-performance servers and databases all of which operate at extreme speeds to do calculations such as these in almost no time. The great thing about it is that the significance or value of the edges could change (instead of representing distance, it would represent travel time by car) yet the algorithm itself would not change. The attribute that a node or edge represents is arbitrary and merely a parameter, defined for the convenience of the user.
This application of graphs in the real world is a small example yet a super important one that are common to people’s lives. A lot of people underestimate the power of graphs and take them for granted. Perhaps the next time you get lost trying to find someplace and resort to using a program like Google Maps, it will be nice to understand and be grateful of the technology and concepts behind it.

Watched Todd play Skyrim for quite a while. Had no idea he was playing PS3 version until he held up controller. So PS3 owners, don’t fret.