Understanding the Foundation of Makeup Wearing using Game Theory
Amidst the marketing formulae, the makeup industries have unceasingly raised people’s standards for appearances by overexaggerating the effect of small imperfections. By promoting beauty products with more and more functionalities, these industries thrive on people’s insecurities. Gail Dines, a sociology professor at Wheelock College said, “If tomorrow, women woke up and decided they really liked their bodies, just think how many industries would go out of business.” So why can’t everyone quit using makeup to save more time, more money, and achieve higher self-esteem? An interesting article by Sukhnidh Kaur discussed the foundation of why people wear makeup using Game theory.
Although the ideal situation is for everyone to avoid wearing makeup, it is not the optimal state we may eventually achieve. If one group wears makeup, the pressure will come on the other group without makeup as they might be perceived as less desirable or attractive. To start our discussion, there are two assumptions that we made about people’s tendency to make up:
- Making up is a time-consuming process and is naturally avoided
- Making up is beneficial to relieve pressure because of a tendency to be more attractive
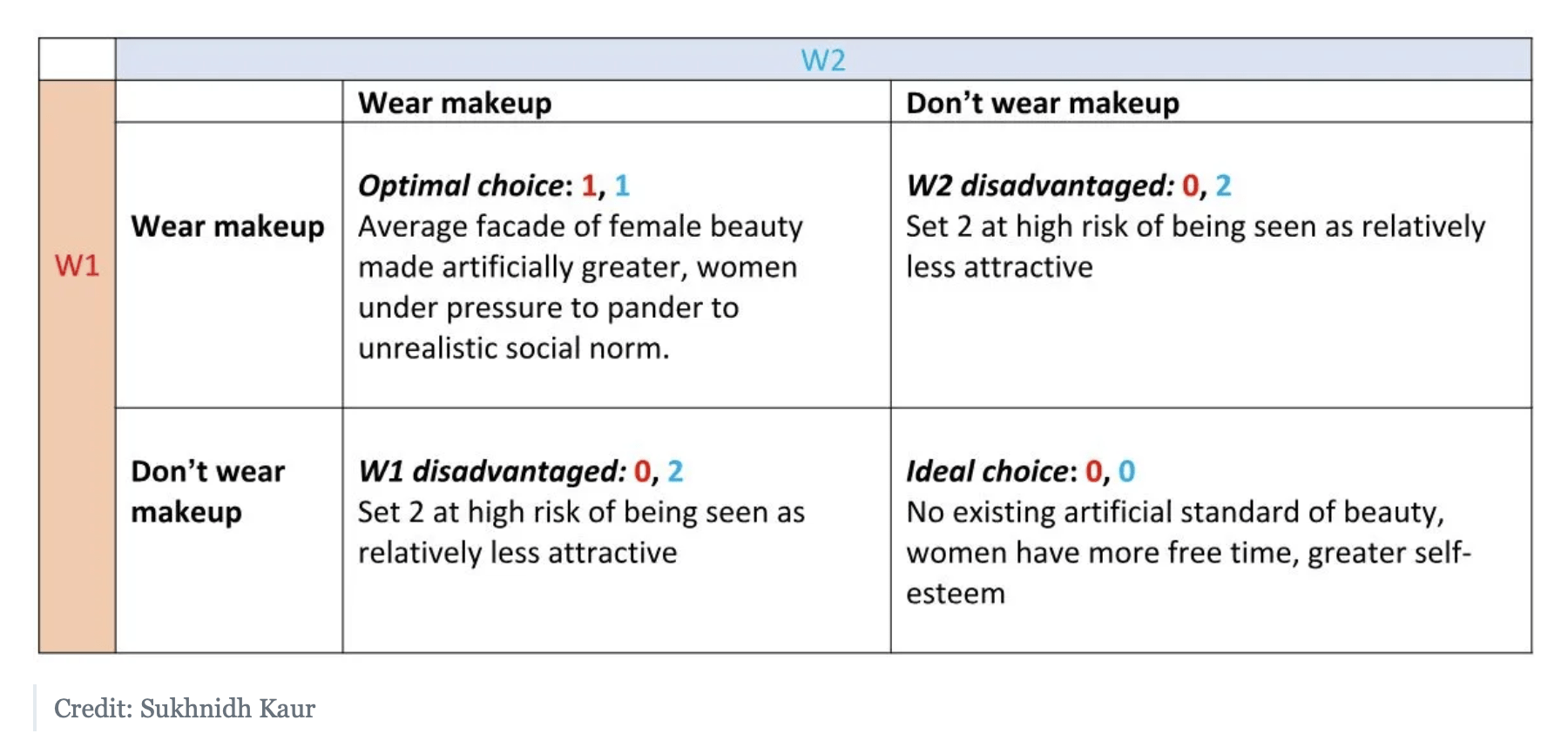
The original article believes the second and proposes the following pay-off matrix from the article illustrates social pressure from wearing makeup. The entry of the payoff matrix is a scale of pressure that ranges from 0 – 2, in which 0 = no pressure, 1 = moderate pressure, and 2 = high pressure.
I catch a mistake in the author’s matrix: on the bottom left corner, when W1 doesn’t wear makeup and W2 wears makeup, W1 will be set at high pressure while W2 has no pressure. Therefore, the correct pay-off for the bottom-left cell should be (2, 0). There are two Nash equilibriums: both players could wear the makeup at the same time, (1, 1), or both players wear no makeup, (0, 0). However, the author believes that in reality, people will end up all wearing makeup because they want to avoid risking high pressure and not everyone is a rational decision-maker.
| Wear Makeup | Don’t Wear Makeup | |
| Wear Makeup | 1, 1
Both suffer from moderate pressure |
0, 2
W2 suffers from high pressure |
| Don’t Wear Makeup | 2, 0
W1 suffers from high pressure |
0, 0
Nobody suffers from pressure |
Corrected Matrix
This is an interesting opinion yet I slightly disagree with it. Since there are two Nash equilibriums, it’s hard to say which one is better than the other without extra information. Alternatively, If we consider a mixed strategy and assume p, q to be the probability that W1 and W2 wear the makeup, respectively, then we will have:
1 * q + 0 * (1 – q) = 2 * q + 0 * (1 – q)
1 * p + 0 * (1 – p) = 2 * p + 0 * (1 – p)
Which gives p = q = 0! This solution is surprising and says that people will actually not wear makeup at all. This actually aligns with the setup of the matrix, since when people are not wearing makeup, they are receiving lower net pressure compared to when they are wearing makeup at the same time. The analysis is flawed in the sense that the payoff matrix is not aligned with the assumptions made by the author.
If we continue on the thread and really believe that assumption (b) is true, we can define a new payoff matrix that illustrates the situation when makeup is mostly for self-satisfaction. In this case, I assume that pressure level is derived from how one compares to the other. Under this scale, if one is happier than normal and suffers from zero pressure, I put a 0. And 1 = normal pressure, 2 = moderate pressure and 3 = high pressure. Since makeup can drive self-satisfaction, now I assume that in a case when a group wears makeup and the other doesn’t, the pressure will be (0, 3). In the case where both wear the makeup, both parties have higher pressure from the extra money and effort than when nobody wears makeup. Now it resembles a prisoner’s dilemma problem, where the only pure Nash equilibrium will be for both individuals to wear the makeup because they want to avoid the risk from (0, 3). Although people could achieve a welfare-maximizing result from not wearing makeup at all, they end up in a Nash equilibrium where both parties suffer from higher pressure.
| Wear Makeup | Don’t Wear Makeup | |
| Wear Makeup | 2, 2
Both suffer from moderate pressure |
0, 3
W2 suffers high pressure while W1 is happy |
| Don’t Wear Makeup | 3, 0
W1 suffers high pressure while W2 is happy |
1, 1
Both suffer from normal pressure |
New Matrix
Despite the flaw of its analysis, the article points out an important assumption of the Nash equilibrium theories: the players should be purely rational and knows the consequences, or “payoffs”, of every possible action they take. This is often not true for human beings, as our choices and tastes depend on our emotions and the payoff of our decisions is not static. For example, if someone is attending a casual event but wears full makeup, it will become very embarrassing and end up with high pressure. On some occasions, participants are expected to dress precisely casually (ex. Business Casual) and any decisions not aligning with the criteria end up in high pressure. There’s no dominant strategy at all that guarantee a better outcome. In reality, the payoff continuously changes with the standards and expectations. We can’t apply a simple payoff matrix or Nash equilibrium in complicated situations like these. However, the game theory mindset could help us make wiser decisions when facing external pressures that were not supposed to exist at the very beginning.
References:
https://livewire.thewire.in/gender-and-sexuality/women-makeup-game-theory/