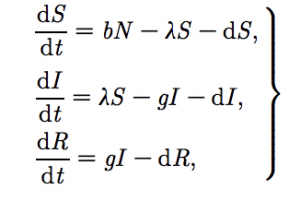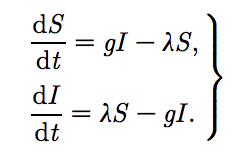Epidemic Models (SIR), (SIS), and Sexually Transmitted Diseases
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1578276/pdf/rsif20050051.pdf
This academic paper – Networks and Epidemic models (2005) – by Matt J. Keeling, and Ken T. D. Eames applies standard epidemic theory and the susceptible-infectious-recovered (SIR) and (SIS) models to discuss sexually transmitted diseases, providing a more complex understanding of the subject than we had time in class.
First, the paper outlines the two standard sets of differential equations that provide the foundation for nearly every mathematical epidemiology study:
The (SIR) model and the (SIS) model:
The authors of the paper acknowledge that these equations and the majority of conventional disease models describe individuals that are susceptible, infected, and recovering from a particular disease completely neglecting the progression of infection and the differences in responses from patient to patient – but nonetheless, the simplification has been accepted for decades.
The susceptible-infectious-recovered (SIR) model presented above (and from our discussion in class) refers to infectious diseases that involve lifelong immunity, like rubella, measles or whooping cough. Meanwhile, the (SIS) model is more frequently used for (STDs), like gonorrhoea, where individuals can get repeatedly infected. We know the S, I and R refer to the amount of susceptible, infectious and recovered individuals, respectively, in a population size denoted as N.
The force of infection, 
, represents the rate susceptible individuals will become infected, and in this model it is a function of the number of infectious individuals. It contains information about the interactions between individuals that lead to the transmission of infection. When the population mixes at random, so that each individual has a small and equal chance of coming into contact with any other individual, the force of infection can be calculated as follows:
This equation might seems complex, but leads to the nonlinear term ( 
SI/N ) which represents the transmission of infection, with which Keeling and Eames explain that they lead to a variety of rich dynamical behaviors.
Lastly, it is important to note that biologically motivated modifications have been made to this basic framework that consider additional heterogeneities by subdividing the S, I and R classification. This either reflects complexities in pathogen biology or host population structure. This breakdown compliments our discussion of the (SIS) epidemic model in class. Make sure to check out Networks and Epidemic models (2005) for more information on this subject.