Networks

Examining Biological Contagion with COVID-19

One class topic I found particularly interesting this year was the idea of epidemic/disease contagion, the rate of transmission across a certain in-contact network, and how it is measured/estimated that a disease will die out after a finite number of steps or spread indefinitely. I wanted to see if this same theory could be applied to the context of diseases in the world that I’ve actually interacted with and see if the model is an accurate predictor of the disease’s probability of living on.

Each disease is assigned some value R0, otherwise known as the Basic Reproductive Number, which is an epidemiological parameter that measures the transmission potential of a disease in a certain population. It is defined as a product product of k, the number of people an infected person meets in a population, and p, the probability that this person infects the number of people they meet independently. If a disease’s R0<1, then the disease isn’t ‘replenishing’ itself and will die out in a finite number of steps with probability 1. If a disease’s R0>1, then the disease is more than ‘replenishing’ itself and will spread indefinitely with probability greater than 0. If you want to reduce R0, you can take measures to reduce p and/or k by reducing the likelihood that the disease can spread or the amount of interaction in the pandemic. To measure this, I will look at a disease that could represent an indefinite epidemic or represent an epidemic that dies out after a certain number of waves. Let’s look at the example of COVID-19, which is an infectious disease caused by the SARS-CoV-2 virus that was discovered in 2019.

Based on an article “Probability of COVID-19 infection by cough of a normal person and a super-spreader” published by Amit Agrawala and Rajneesh Bhardwaj in 2021 (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7976050/), the probability of infecting someone with COVID-19 depends on a number of factors including distance and the use of protective equipment like masks. In the situation that we are trying to model, we want to look at the original R0 of COVID-19 without preventative measures (like introducing masks), so assuming that an infected person on our model comes within a distance of 0.5 meters of another person, p=0.5. Let’s also assume that we’re trying to model the transmission potential of COVID-19 in a high school of about 500 people, where an infected person would be likely to come into contact with 100 of these people while sick, thus making k 100. In this situation, the model predicts that R0 = (0.5)(100) = 50, which is greater than 1 and therefore the disease would continue to spread indefinitely. 

Now imagine that preventative measures are introduced to stop the spread of the disease in two ways: 1) by introducing protective equipment like masks and 2) by implementing a home-quarantine for students (which is consistent with the response that was taken to COVID-19 epidemic in real life.) In this case, the probability of transmission at a distance of 0.5 meters with a surgical mask is 0.1. During an at home quarantine, we can assume that the average number of people that an infected person could interact with is 3, which is our k. In this situation, the R0 = (0.1)(3) = 0.3, which is less than 1 and, therefore, contains the spread of the disease and reduces the epidemic to a finite number of waves. Contextually, this model is consistent with the spread of COVID-19 in real life before and after the introduction of preventive measures.

Game Theory in Online Marketplaces: Navigating the Complex Dynamics of eBay and Amazon

The application of game theory in online marketplaces like eBay and Amazon has revolutionized how sellers and buyers interact, particularly in terms of pricing and reputation management. 

On Amazon, the intricate dance of pricing is where game theory really comes into play. Tools like Seller Snap utilize game theory to optimize repricing strategies, a crucial aspect for sellers vying for the coveted Buy Box. Traditional repricers often trigger a race to the bottom, where prices continually drop as sellers underbid each other. However, game theory-based repricers like Seller Snap aim for a more balanced approach. They analyze competitors’ pricing strategies, seeking an equilibrium that maximizes profit without initiating a price war. This approach considers the individual motivations and strategies of each seller, recognizing that every decision in a competitive marketplace like Amazon impacts and is impacted by others’ actions. It’s about understanding the circular nature of pricing decisions and finding a stable position that benefits all parties involved.

eBay’s reputation system is another area where game theory offers insights. The platform’s feedback mechanism encourages cooperative behavior between buyers and sellers. A good reputation becomes a valuable asset, influencing future transactions. Sellers with higher ratings are more trusted, leading to more sales, while buyers with good reputations are more likely to be trusted by sellers. This reciprocal system, rooted in game theory principles, ensures a stable and trustworthy marketplace environment.

Consider a scenario where two sellers, A and B, are offering the same product on Amazon. Both sellers aim to win the Buy Box, which significantly increases their chances of making a sale. In this situation, each seller has to decide on their pricing strategy, taking into account how the other seller might react.

If Seller A decides to lower their price, Seller B has to decide whether to match or beat this new lower price to remain competitive. If both sellers continue to lower their prices in response to each other, this leads to a race to the bottom, where eventually both may end up with minimal profits. However, using game theory, Seller A might predict that lowering the price will lead to this undesirable outcome and instead opt to maintain or slightly increase their price. If Seller B recognizes this strategy and also decides not to engage in a price war, both sellers can potentially maintain reasonable profit margins.

Seller Snap’s approach to repricing on Amazon encapsulates this strategy. Instead of aggressively trying to undercut competitors, it aims to find a balance, considering the strategies of other sellers. This approach can avoid continuous price dropping, seeking a stable pricing equilibrium that benefits all parties involved. The tool can analyze the price history of a listing or make experimental price changes to understand how competitors react, thereby figuring out their repricing strategies and adjusting accordingly​​.

In these online marketplaces, the dynamics of game theory are evident in how sellers and buyers strategically interact. It’s not just about the immediate transaction, but also about understanding and anticipating the actions of others in a complex web of interdependencies. This strategic thinking, influenced by game theory, is what makes eBay and Amazon fascinating and constantly evolving ecosystems.

 

References: https://www.webretailer.com and https://www.jstor.org

 

Sustainable Practices as Evolutionarily Stable Strategies

One topic I found particularly interesting from Networks 2040 is the concept of evolutionarily stable strategies, or ESS. By definition, if adopted by a population, an ESS resists being overtaken by an alternative strategy due to providing the best benefit when used against itself, making it stable and self-reinforcing. While studying this concept, I felt a strange sense of familiarity within it. Eventually I grew to realize that I work on creating such strategies everyday.

This phenomena of biological evolution easily applies to the physical strategies of mankind in that we constantly seek mechanisms to enhance and innovate aspects of daily life, from creating climate controlled shelters, advancing medicine in health care and the overall optimization that the modern day brings. All of these concepts can be considered ESS in their own right.

However, as an environmental engineer, we focus on creating solutions that specifically enhance the resilience and stability of such strategies. Sustainable energy solutions empower us to continue innovation without the heavy expense of fossil fuels. Water conservation and management allow for the optimal health and distribution of the most vital life resource: water. Finally, environmental engineers focus on creating circular economy models that promote self-sufficiency and long-term reliability. The intersection of ESS and engineering allows us to create brighter, promising strategies for the future.

Networks 2040 has been an incredibly fulfilling experience. The exposition to the concepts of network theory has been fascinating and deceptively ingraining. I’ve found many strategies noticeable in everyday life and deepen my understanding of my more technical engineering classes. Thank you all for a wonderful semester!

Using game theory to help a squash player improve their game

 

Squash is a high-speed, intense racket sport played by two players in a four-walled court. The game involves players taking turns to hit a small, hollow rubber ball onto the front wall, while one can use the other three walls as well. The primary objective is to play the ball in a manner that makes it difficult for the opponent to make a valid return, thereby scoring points. It is the only racket sport that is not played across a net.

 

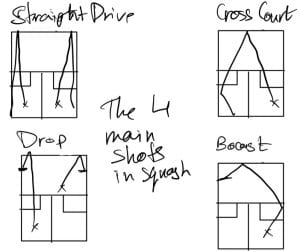
Squash involves a variety of shots, each with its strategic importance:

• A straight drive A basic shot hit straight down the wall to the back of the court. It is mainly used for defense, but it can also make the opponent give you a weak shot/ lose the point if its too deep down the length of the court.
• Cross Court: A shot hit from one side of the court to the other, traveling diagonally across the middle. It’s used to move the opponent across the court. Same purpose as straight drive.
• Drop: A delicate, soft shot aimed just above the tin (like what the net is in tennis), landing close to the front wall, primarily used to catch the opponent off guard, move them to the front of the court, which is tough to pick up and can make one win the point.
• Boast: A shot using the dimensions of the court where the ball is hit against one of the side walls before it reaches the front wall, used for both defensive and attacking plays.

Game Theory and Payoff Matrix

Game theory, in the context of sports like squash, involves strategic decision-making where each player anticipates and responds to the strategies of their opponent. A key concept in game theory is the payoff matrix, a table that shows the payoffs for each player for every possible combination of strategies. It helps in visualizing the outcomes of different strategies and in making strategic decisions.

 

Analysis of a Squash Game

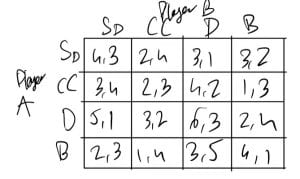
To analyze the squash match between Player A and Player B, where Player A wins 3-2 with the scores 11-7, 8-11, 11-8, 11-13, 11-9, we can create a 4×4 payoff matrix. This matrix will represent each player’s success with different shots: Straight Drive (D), Cross Court (C), Drop (Dp), and Boast (B). The values in the matrix will reflect the number of points each player won with these shots.

 

To analyze the squash match between Player A and Player B, where Player A wins 3-2 in a best of 5 match with the scores 11-7, 8-11, 11-8, 11-13, 11-9, we can create a 4×4 payoff matrix. This matrix will represent each player’s success with different shots: Straight Drive (D), Cross Court (C), Drop (Dp), and Boast (B). The values in the matrix will reflect the number of points each player won with these shots.

 

First, let’s calculate the total number of points played in all five games:

– Game 1: 11 (Player A) + 7 (Player B) = 18 points

– Game 2: 8 (Player A) + 11 (Player B) = 19 points

– Game 3: 11 (Player A) + 8 (Player B) = 19 points

– Game 4: 11 (Player A) + 13 (Player B) = 24 points

– Game 5: 11 (Player A) + 9 (Player B) = 20 points

– Total: 100 points

 

Now, let’s create the payoff matrix with the values from an analysis of the match. Each +1 is the number of points the player won on that shot in response to the other player’s shot.

In this matrix:

– The cell (SD,S D) indicates that when both players played Straight Drives, Player A won 4 points while Player B won 3 points.

– The cell (D, D) shows that when both players played Drops, Player A was more successful, winning 6 points compared to Player B’s 3 points.

– eg interpreting (SD, D) in instances where Player A hit a Straight Drive (SD) and Player B hit a Drop (D), the outcome was that Player A won the point 3 times, and Player B won it once. It shows that player 

 

This interpretation of the matrix helps in understanding how each player’s choice of shot impacted the game’s outcome in specific situations. It indicates that in this particular match-up (Straight Drive by Player A vs. Drop by Player B), Player A had a strategic advantage.

 

This matrix provides a framework for analyzing the effectiveness of different shots and strategies employed by each player during the match. By studying the payoffs in various scenarios, coaches and players can gain insights into which shots were most effective and how the players might adapt their strategies in future games.

 

This analysis demonstrates the strategic variety in squash and how players’ choices of shots impact their game performance. The use of game theory and payoff matrices provides valuable insights into the decision-making process in competitive sports like squash, helping players and coaches devise more effective strategies for winning. This can be integrated into the training schedule of players.

 

• For each of Player A’s strategies, we look for the best response by Player B.
  • When Player A plays a Straight Drive, Player B’s best response is a Cross Court (A:2, B:4).
  • When Player A plays a Cross Court, Player B’s best response is a Straight Drive (A:3, B:4).
  • When Player A plays a Drop, Player B’s best response is a Boast (A:2, B:4).
  • When Player A plays a Boast, Player B’s best response is a Drop (A:3, B:5).
• Conversely, for each of Player B’s strategies, we find Player A’s best response.
  • When Player B plays a Straight Drive, Player A’s best response is a Drop (A:5, B:1).
  • When Player B plays a Cross Court, Player A’s best response is a Drop (A:3, B:2).
  • When Player B plays a Drop, Player A’s best response is also a Drop (A:6, B:3).
  • When Player B plays a Boast, Player A’s best response is a Straight Drive (A:3, B:2).

Looking at these responses, it seems there is no pure strategy Nash Equilibrium in this matrix. In a Nash Equilibrium, both players’ strategies would be best responses to each other, but this doesn’t occur in any of the shot combinations here.

Interpretation for Players A and B:

• The absence of a pure strategy Nash Equilibrium suggests that there is no single combination of shots where both players would find no benefit in unilaterally changing their strategy.
• This indicates a dynamic and unpredictable nature of the game, where players need to continuously adapt their strategies based on the ongoing play.
• It suggests that both players might need to consider mixed strategies (a combination of different shots) rather than relying on a single type of shot throughout the game.
• The matrix highlights the strengths and weaknesses of each player against specific shots, offering insights into potential areas of improvement and strategy development for future games.

 

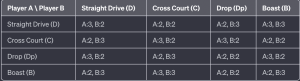
Finding any strategy being strictly dominated means that shot leads to lower payoffs in every situation To determine if any strategy is strictly dominated in the given matrix, we need to compare each strategy’s payoffs to see if one strategy consistently results in a worse outcome than another, regardless of the opponent’s actions.

 

Analyzing Player A’s strategies:

– Straight Drive (SD) vs. Cross Court (CC): D yields more points against Player B’s D and C, but less against Dp and B.

– Straight Drive (SD) vs. Drop (D): Dp yields more points against all of Player B’s strategies.

– Straight Drive (SD) vs. Boast (B): B yields more points against Player B’s C and Dp but less against D and B.

– Cross Court (CC) vs. Drop (D): Dp yields more points against all of Player B’s strategies.

– Cross Court (CC) vs. Boast (B): No consistent superiority.

– Drop (D) vs. Boast (B): Dp yields more points against Player B’s D and C, but less against Dp and B.

 

From Player A’s perspective, the Drop (Dp) strategy strictly dominates both the Straight Drive (D) and Cross Court (C) strategies. This makes sense because the drop shot is one of the toughest shots to pick up. 

 

Analyzing Player B’s strategies:

– Straight Drive (SD) vs. Cross Court (CC): D yields more points against Player A’s D and C, but less against Dp and B.

– Straight Drive (SD) vs. Drop (Dp): Dp yields more points against Player A’s D and B, but less against C and Dp.

– Straight Drive (SD) vs. Boast (B): No consistent superiority.

– Cross Court (CC) vs. Drop (D): Dp yields more points against Player A’s D, but less against C, Dp, and B.

– Cross Court (C) vs. Boast (B): B yields more points against Player A’s Dp and B, but less against D and C.

– Drop (D) vs. Boast (B): No consistent superiority.

 

From Player B’s perspective, no strategy is strictly dominated by another.

 

Conclusion:

– For Player A, the Drop (Dp) strategy strictly dominates both the Straight Drive (D) and Cross Court (C) strategies.

– For Player B, there is no strategy that is strictly dominated by another. 

 

This analysis suggests that Player A might consider focusing more on the Drop shot, given its overall effectiveness compared to other strategies. However, Player B does not have a clear strategy that is consistently outperformed by another, indicating a more balanced range of effective shots.

 

Lets consider a different match with these payoffs:

In this adjusted matrix, no single strategy strictly dominates another for either player, and there’s no clear pure strategy Nash equilibrium. This setup suggests that a mixed strategy Nash equilibrium might exist.

What a Mixed Strategy Nash Equilibrium Means in this Context:

A mixed strategy Nash equilibrium in the context of squash implies that players will randomize their shot selection, choosing different shots according to specific probabilities that make their opponent indifferent to their own shot choices. In other words, each player mixes their strategies (shot types) in a way that their expected payoff is maximized given the mixed strategy of the opponent.

For Player A and Player B, this means:

• Neither player will settle on a single type of shot as their constant strategy.
• They will vary their shots, keeping their opponent guessing and unable to predict the next move reliably.
• The probabilities with which they choose each shot type are calculated so that changing their strategy wouldn’t give them a higher expected payoff, given the strategy of the other player.

In practical terms, this reflects a highly dynamic and unpredictable game where players continually adapt their strategies, and the game doesn’t settle into a predictable pattern. The mixed strategy equilibrium represents the players’ optimal response to the uncertainty and complexity inherent in their opponent’s shot selection.

 

Social Networks’ Role in Product Adoption

The rise of ChatGPT earlier this year surprised all of us, but the underlying forces driving its popularity are rooted in social networks. I wanted to talk about how brand communities, which are on a smaller scale than social networks, have a significant impact on product adoption. Using network theory, we can see how community members and their interactions form a network that has a significant impact on the dissemination of information about new technologies such as ChatGPT. The phenomenon of information cascades is especially noticeable here, where adoption decisions made by influential members ripple through the network, shaping overall product acceptance. This reflects larger patterns of influence and decision-making in social networks, demonstrating the significant influence these structures have on consumer behavior and technology acceptance.

Peer influence is crucial in these networks, particularly among younger demographics such as Generation Z. Research says that an individual’s likelihood of adopting a new product increases if their peers have already done so. This effect is heightened in the digital age, where information and experiences shared through these networks greatly increase the appeal of new technologies. As a result, the significance of social proof in product adoption is emphasized, emphasizing the critical role of peer influence in the acceptance and widespread use of technological innovations. I conducted research of my own last semester and found overlapping trends and use cases by GenZ, demonstrating how quickly our generation can get influenced.

Businesses and organizations can use this understanding of social networks and peer influence to improve their marketing strategies. They can create advocates who will organically spread information and positive feelings about their products, by engaging with and fostering brand communities. Targeting key influencers within these networks can cause information cascades, increasing product visibility and adoption significantly. Understanding these dynamics enables businesses to effectively position their products in the market, especially in high-digital-engagement industries.

 

History of Nash Equilibrium: Discovery and Use Today

Overview

Discovered by American mathematician, John Forbes Nash, Jr., Nash equilibrium is a fundamental concept in game theory that illustrates decision-making in players based on their interactions with others. The main purpose is to optimize a player’s outcome by taking into account other players’ decisions. Nash equilibrium is achieved when neither player—in a two player game—has any incentive to deviate from their strategy. This holds true even when both players know the other’s strategies. By using Nash equilibrium, we can model economic behaviors and predict best responses to given scenarios.

John Forbes Nash, Jr. and Nash Equilibrium

Regarded as one of the greatest mathematicians of the 20th century, John F. Nash, Jr. was a genius when faced with mathematics. He was known for his originality and boldness when facing seemingly unsolvable problems. Throughout his life and career, he introduced numerous concepts that are now central to game theory and mathematics. He first began his work on equilibrium theory during his time at Princeton University while pursuing graduate studies in mathematics and sciences. In 1950, he earned a PhD with his 27-page thesis on non-cooperative games which provided a way to predict game outcomes while maximizing self-interest: Nash equilibrium. This dissertation contained the definition and use of the Nash equilibrium which is crucial to understanding non-cooperative games. 44 years later, he received the Nobel Memorial Prize in Economic Sciences for his work in game theory. This single concept has greatly changed the analysis of competitive situations. Roger Myerson, an economist at the University of Chicago, compared the impact of the discovery of Nash equilibrium to that of “the discovery of the DNA double helix in the biological sciences.” From business rivalries to policy-making, Nash equilibrium has become instrumental in the social sciences and continues to make headway in other fields.

Before Nash and game theory, economics was largely based on the theory of supply and demand and Keynesian economics. However, this could only be broadly applied to the dynamics of markets with many buyers and sellers. The dynamics of particular industries and businesses still lacked in theory and research. When examining how competition existed between businesses or how bidders decided to bid, economists had little progress. The first people to develop game theory were von Neumann and Oskar Morgenstern. They provided the framework for analyzing such situations, but they were only able to determine “equilibria” for situations with a definite winner and a definite loser. This failed to apply to real world situations where a definite winner or loser often did not exist. Instead, multiple competitors could have positive payoffs depending on the strategies they used. Nash began developing his equilibrium theory by starting out with a solution to games where each player performs the best to their ability, given the strategies of other players. Using his solution and the mathematical theory developed by L. E. J. Brouwer, a Dutch mathematician, Nash was able to demonstrate that his theory of equilibrium existed in any game with finite players and strategies. Despite being dismissed by von Neumann, Nash’s theory of equilibrium became one of the most widely known concepts in game theory and economics. To this day, students and economists alike use Nash equilibrium to solve for best responses and rule out illogical answers. As research continues in different fields, Nash equilibrium may eventually extend well beyond its current applications in economics.

An Information Cascade Through Reddit

In the era of digitization, the notion of the information cascade is gaining more prominence, and the Reddit online community serves as a captivating illustration. Reddit, an extensive network of forums where individuals exchange news and content, acts as a fertile breeding ground for the dissemination of knowledge. Users’ contributions are subjected to voting, which influences the visibility and popularity of the content. While this system promotes fairness, it can also facilitate the swift propagation of information based on popularity rather than accuracy. The identification of the 2013 Boston Marathon bombings serves as a noteworthy case in point. Reddit users, stepping in to assist, commenced sifting through publicly accessible photos and videos from the marathon. This collaborative investigation swiftly escalated into a cascade of information, as users began singling out individuals whom they found suspicious. These individuals’ names and images garnered a substantial number of votes, leading many to adopt these conclusions without subjecting them to critical analysis or official confirmation. This scenario epitomizes the potential detriment of an information cascade. As an increasing number of users adopt and disseminate these conclusions, the conviction regarding their accuracy intensifies, disregarding the absence of solid evidence. Consequently, innocent individuals become subject to false accusations, resulting in distress and bewilderment.

This Reddit example underscores the ambivalence of information cascades within online communities. While they can efficiently mobilize resources and knowledge, they can simultaneously facilitate the rapid dissemination of misinformation. This accentuates the necessity of cultivating critical thinking and validation in the digital age, where the demarcation between factual information and speculative content can easily blur in the face of information cascades.

Source: https://academic.oup.com/bjc/article/57/2/341/2623876

Networks in Activism

As technology advances, networks and communication continue to evolve and change. The world we experience today is drastically different from the world in which the previous generation grew up. Over the years, the ratio of strong and weak ties that people typically have has shifted. In the past, people generally had a few strong ties, mainly with close friends and family. People also had several weak ties, often with neighbors, colleagues, classmates, etc. Today, people have similar amounts of strong ties as the previous generation. However, the introduction of social media and online communication have allowed people to have large amounts of weak ties. New technologies, such as social media platforms and mobile communication, have allowed people to connect with others around the world, vastly expanding people’s networks. However, this can hinder individual connections, because people are distracted and preoccupied with other connections. Although people now have many acquaintances, we do not necessarily have closer relationships than in the past. Qualities such as trust, support, and accountability are found only in strong ties. At the same time, weak ties can provide new perspectives, skills, and information that we would otherwise not be exposed to.

Weak ties can allow for the diffusion of innovations, as well as the spread of information. Many people have began to take advantage of the networks formed through social media platforms, using them to raise awareness and promote social causes. Researchers have observed the strong influence that peers have on an individual. Just as people often have a threshold for adopting a new technology, some people have a threshold for supporting a certain social movement. People have both an expressive utility, the desire to say what one thinks, and a reputational utility, the desire to be respected by others. One’s reputational utility can often overpower their expressive utility. This strong peer influence makes networks a key component in the success of social movements.

Strong Triadic Close Can Be Dangerous

In the intricate web of social networks, the concept of ‘strong triadic closure’ is a fundamental principle that explains how relationships evolve and solidify. This principle states that if two people have a strong relationship with a mutual friend, they are likely to develop a strong relationship with each other. While this phenomenon fosters community building and supportive environments, it also harbors a lesser-discussed implication: the potential for unhealthy habits to spread. 

 

The reason behind this phenomenon is the power of influence that strong ties wield in our lives. People we are strongly connected to, like close friends or family, have a significant impact on our behaviors, attitudes, and choices. We are more likely to mimic or adopt the behaviors of those we spend most time with, especially if we admire or respect them. This is the fundamental principle behind the theme that we are all byproducts of our environment.

 

This brings us to an essential point: the importance of being mindful of who we form strong connections within our social networks. While it’s not practical or desirable to only form connections with ‘perfect’ individuals (as no one is without flaws), it is crucial to be aware of the habits and lifestyles of those we are close to. When thinking about who you hope to be in the future, look around at who you spend time with and realize that you will also be introduced to even more people with these traits.

 

One proactive approach is to foster and nurture relationships with individuals who display positive habits and traits. Being around people who prioritize healthy lifestyles, positive mental attitudes, and constructive behaviors can significantly influence us to adopt similar habits.

 

It’s also vital to balance our relationships. While it’s beneficial to have close, strong ties, it’s equally important to have a diverse range of connections. Connecting with people of different backgrounds and lifestyles can prove to be extremely valuable. This diversity can provide a buffer against the potential negative influence of any single group or individual. 

 

Overall, the main message I hope you take away from this is the importance of surrounding yourself with people you hope to be more like. Networks can be useful in assessing your current situation and making connections about why you have developed certain habits.

Digital Platforms and Network Effects

I took “Analyzing Digital Platforms” with Professor Michael Maffie, and to my surprise network effects was a huge topic of discussion and revealed to be the foundation of several digital platforms we analyzed. 

I learned that a platform is a business model that facilitates the exchange of value between two or more user groups, a consumer and a producer. In order to make these exchanges happen, platforms harness and create large, scalable networks of users and resources that can be accessed on demand. Platforms create communities and markets with network effects that allow users to interact and transact. Johnson and Moazed explain how network effects occur when the value of the platform increases with the number of users. As more users join the platform, there’s a positive feedback loop that attracts even more users. This drives rapid growth, enhances the platform’s value, and leverages economies of scale. (Johnson and Moazed) Networks are the new aggregator of business value, when the world becomes more connected what a company owns matters less than the resources it can connect to. Today’s most valuable businesses are those that can build and orchestrate large networks, not those that can aggregate and centralize large amounts of resources under one roof. Platforms are often defined by the network that surrounds it, without its consumers and producers, platforms wouldn’t exist. Many digital platforms, especially social networks and communication platforms, benefit from network effects. Network effects occur when the value of the platform increases with the number of users. As more users join the platform, there’s a positive feedback loop that attracts even more users. This drives rapid growth, enhances the platform’s value, and leverages economies of scale. Platform companies like Amazon, Google, Facebook, and Apple have achieved a level of economic scale and market dominance that allows them to shape and control the way consumers and other businesses interact with their platforms.  In contrast to traditional business models based on selling goods or services, platform companies represent a new means to create and capture value through their capacity to harness an immense amount of data in ways that allow them to rule the market . Platform business models enable companies to expand at a pace unprecedented in human history, in other words, platforms grow exponentially rather than linearly. Platform businesses are more cost effective and higher scale than old models. Four functions of a platform: audience building, matchmaking, providing core tools and services, setting rules and standards. Amazon connect buyers with sellers, and information platforms like Facebook and Google connect people to each other, to advertisers, and to information.  Lehondrivta also mentions that it is the concept of economy of scale in which the unit cost of doing something goes down as the quantity goes up. Amazon enjoys economies of scale over regular brick and mortar stores. Platforms like Amazon and Google are so ingrained within our society that politicians are scared to regulate them; Culpepper and Thelen highlight that these companies have truly become so integral to people’s daily lives. For example everyone uses Amazon’s fast delivery service (Amazon Prime) and Facebook’s role as an information gateway connect consumers to essential services and information. Politicians are wary of being seen as the ones who might disrupt these convenient and popular services. Bezos said that he would step down if there was a new platform to replace amazon and eventually he did, he is now focusing on a space technology company that he founded.

Moazed, A., & Johnson, N. L. (2016). Modern monopolies what it takes to dominate the 21st-century economy. MarmotLibraryNetwork. https://gcld.marmot.org/Record/.b57228280

keep looking »