Physical Review E, 2013: Force and Flux Relations for Flows of Ionic Solutions between Parallel Plates with Porous and Charged Layers
Citation:
Barbati AC, Kirby BJ. Force and Flux Relations for Flows of Ionic Solutions between Parallel Plates with Porous and Charged Layers, Physical Review E, 88:042408, 2013. doi pdf
Abstract:
We derive coefficients of the electrokinetic coupling matrix (x11, x12, and x21) for the flow of an ionic solution through a parallel-plate geometry having porous and charged layers grafted onto a solid surface with a known potential and demonstrate Onsager reciprocity for the cross terms (i.e., x12=x21). Our results enable the prediction of system outputs in the solid-porous-fluid system from parameters that are either known or may be measured and inferred. These electrokinetic coupling coefficients are in terms of the potential and fixed charge only, removing dependence on field gradients and fluid velocity. Additionally, we present simplified expressions of these coupling coefficients in limiting regions of the parameter space. Away from these limits, we present numerical results demonstrating the facility of our functional form for facile numerical approximation and report the utility and accuracy of our analytical approximations.
Figures:
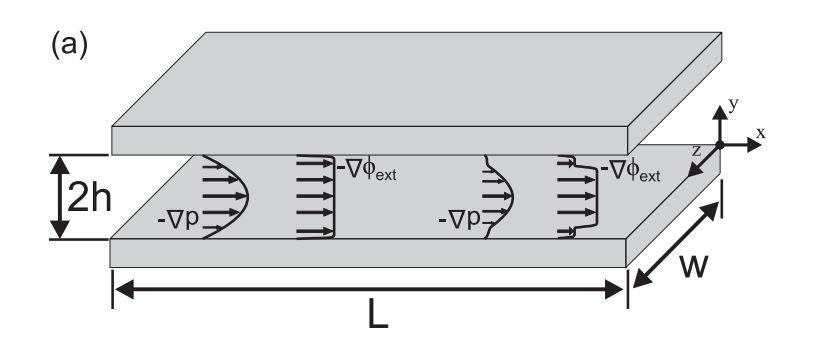
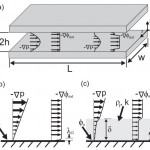
- FIG. 1. Diagrammatic representation of the system under consideration. (a): Geometric definition of the parallel-plate system studied; plates of width w and lengthLare separated by a distance 2h. Included are shapes of pressure-driven and electrically forced flows for (left) a channel with rigid surfaces and (right) a channel with a porous lining. In (b) and (c), magnified diagrams at the surface detail distributions of velocity and potential for a bare, rigid surface (b) and a surface with a porous layer of thickness delta(c).doi pdf
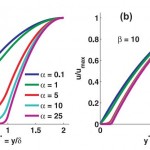
- FIG. 2. Velocity profiles about the channel centerline for varying layer resistance parameter α and relative channel height beta. At left, beta = 2, the velocity profile is strongly perturbed from parabolicity by large and moderate values of alpha. At right, beta = 10, the channel is large relative to the porous layer thickness, and retarding effects are mainly confined to the porous layer and do not interfere strongly with momentum transport in the pure fluid region. doi pdf
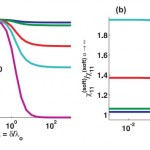
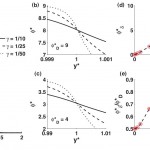
- FIG. 3. Plots of x(soft)11 normalized by the alpha to 0 limit (left) and the alpha to infinity limit (right). In both cases, porous layer effects are small when the channel height is large relative to the porous layer thickness (beta>> 1). doi pdf
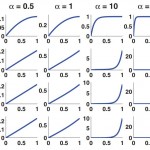
- FIG. 4. (Color online) Behavior of the filterlike function as function of space over a range of alpha (columns) and beta (rows). The horizontal axes in all plots range over 0 to 1. doi pdf
- FIG. 5. Numerical results for electrical potential distributions and comparison against exact results. doi pdf
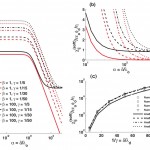
- FIG. 6. Behavior of the coupling coefficients x(soft)12 and x(soft)21 over seven decades of alpha for beta = 1 [red lines in (a) and (b)], beta = 100 [black lines in (a) and (b)], and various values of gamma, indicated with various line styles. Panel (c) compares numerical values and analytical approximations of x(hard) in the alpha<1 limit. doi pdf
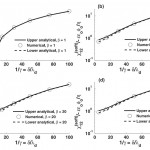
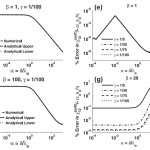
- FIG. 8. [(a) through (d)] Large-alpha limit applied over the entire range of alpha. [(e) through (h)] Errors (as percentages) in x(soft)12 applied over the entire range of alpha. The nonmonotonicity observed in the errors is results from taking the maximum error of the difference between the numerical value and upper and lower estimations of x(soft)ij . doi pdf