Common Knowledge: Coordination Games Revisited
As we have learned in class, a coordination game is a game where all players get a positive payout if they choose the same strategy, but nobody gets any payout if a player chooses something different from the rest. The following table shows an example of a coordination game:
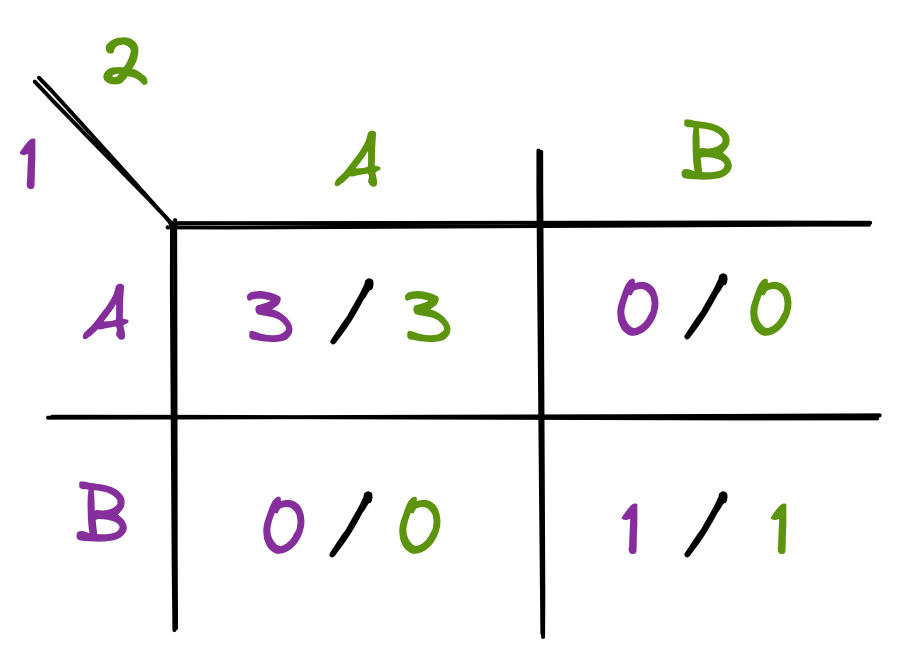
If Player 1 chooses A and Player 2 chooses B or vice versa, then neither gets a reward, making this a coordination game. If both choose A, then they both receive a payoff of 3, and if both choose B, then they both receive a payoff of 1. Because the payoffs when all players coordinate depend on the strategy they both take together, this example is an unbalanced coordination game.
Now imagine a world playing this coordination game over an extended period of time where both players are currently choosing B. Without any knowledge of how the other player is going to act, neither has an incentive to switch to the other option. This makes (B, B) a Nash equilibrium, and following the same line of reasoning but for both players choosing A reveals that (A, A) is a Nash equilibrium as well. Although both are equilibria, (A, A) is more desirable for both players than (B, B) because it has a higher payoff for both.
How can the players in this world coordinate to move from the worse of the equilibria to the better one? If the game were one-shot, then Thomas Shelling’s idea of a focal point could help the players decide. But the game is already being played! In order to switch equilibria, the players must establish common knowledge and coordinate to switch their strategy of choice at the same time.
But what exactly is common knowledge? The formal definition is quite tricky. A piece of information is common knowledge among a group of people if everyone knows it, everyone knows that everyone else knows it, everyone knows that, and so on (paraphrased from Wikipedia).
The definition is quite the mouthful, but fortunately, The Costly Coordination Mechanism of Common Knowledge provides an excellent example of a role common knowledge plays in the world: unwanted dictators and freedom of speech. Here, the players are people who dislike the current regime, and the strategies are rebel (R) or do nothing (N). Currently, the players are stuck at the (N, … , N) equilibrium, which is much less preferred than the (R, … , R) one. What makes this an unbalanced coordination game is that if only a couple people choose to rebel, then they likely won’t be able to overcome the local police force, much less the dictatorship as a whole (and are also very likely to be imprisoned, tortured, killed, etc).
By establishing communication with everyone else and making each individual declaration of rebellion common knowledge, however, the group can collectively jump straight to the (R, … , R) equilibrium, skipping through the ineffective and deadly corners of the game matrix and (at least having the best odds of) overthrowing the unwanted dictator. This is precisely why dictatorships throughout history have attempted to suppress freedom of speech: dissenters struggle to establish common knowledge when their speech is restricted, remaining in the worse of the two equilibria—under the dictator’s rule.
