Communication and Deception – Game Theory in “Golden Balls”
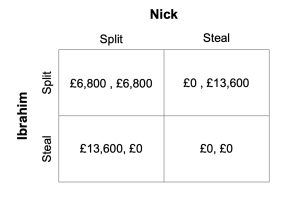
In the British gameshow “Golden Balls”, contestants compete to win as much money as possible by choosing balls containing prizes from £10 to £75,000. In the final round of the game, the two remaining contestants must each choose whether to “split” or “steal” the jackpot. If both choose to split, the each contestant takes home half of the money in the jackpot. If one chooses to split while the other chooses to steal, the one who chose to steal receives the entirety of the jackpot. If both choose to steal, no one receives any money at all. This is a variation of the prisoner’s dilemma game in which the players can either choose to cooperate or cheat. In the video included below, Ibrahim and Nick are playing “split or steal” on a jackpot of £13,600. Their payoff matrix is as follows:
In this case, three Nash equilibria technically exist: (Split, Steal) (Steal, Split) and (Steal, Steal), however it is reasonable to assume that each player would slightly prefer to steal if their opponent chose to as well in order to avoid looking like a fool and allowing the opponent to win. This means both players are incentivized to choose “steal” in this game. Unlike the prisoner’s dilemma game, the players are permitted to discuss their strategy before choosing. In this stage of the game, most players attempt to convince their opponent that they are trustworthy and are certainly going to choose “split”. Even after communicating their intentions to split the jackpot, each player is still incentivized to choose “steal”.
In this case, Nick chooses an unusual strategy. Immediately, he says “trust me, 100%, I am going to choose steal,” and “I want you to do split and I promise you I’ll split the money with you.” This is met with laughter from Ibrahim and the audience. Nick goes on to describe how he will split the money with Ibrahim after the show is over and the host reaffirms that Nick would technically have no legal obligation to do so. Ibrahim attempts to convince Nick that he is a man of his word and will choose split only if he does so as well. Despite this, Nick continues to insist that he will chose “steal” no matter what and that if Ibrahim chooses to steal as well, they are both guaranteed to walk away with nothing.
With this strategy, Nick is effectively forcing Ibrahim to choose “split”. From Ibrahim’s perspective, he (Ibrahim) can either choose to steal and guarantee he gets nothing for himself, or split and hope that Nick follows through and splits the money afterwards. Ibrahim tries repeatedly to convince Nick not to do this, first by appealing to his sense of morality and eventually by calling him an idiot, but Nick never changes his mind. Eventually, the host tells them they must make their decisions and both players lock in their choice. To everyone’s surprise, both players choose “split.”
Nick was able to use deception in order to ensure he received the outcome he wanted. He was going to choose “split” all along but knew the only way to absolutely ensure that Ibrahim would chose “split” was to convince him that it was his only option (and that lying and choosing “steal” instead would only make him worse off). It is a great example of fully understanding the rules of a game theory scenario and taking advantage of your ability to communicate.