Asymmetric Information Equilibrium In Options Markets
Options are financial derivatives based on the value of an underlying asset. A call option gives the holder the right, but not obligation, to buy a particular quantity of the asset at a particular price (known as the ‘strike price’) on or before the expiration date. A put option gives the holder the right, but not obligation, to sell a particular quantity of the asset at the strike price on or before the expiration date. If an option is “In the money”, meaning the value of the underlying asset has increased past the strike price for a call option, or decreased below the strike price for a put option, then the option holder has the right to exercise their contract. This means that the seller is obligated to sell (for a call) or buy (for a put) the agreed upon quantity of the asset from/to the option holder at the strike price. Being called upon to fulfill this obligation is known as “assignment”.
In the options market, as with many other financial markets, all participants do not have equal information. Among quantitative traders specifically, information asymmetry is magnified by unequal access to market data. Since exchanges sell data at relatively high prices, small quantitative trading firms find it difficult to compete with their larger competitors if they are not willing to spend substantial amounts of capital on high-quality data. In addition, while two firms can have the same data, one can mine more information from the data if they choose to use more effective feature selection methods in their machine learning models. This post will examine how the concept of asymmetric information equilibrium can be applied to options trading.
Options become more valuable when the volatility of the underlying security increases, since this means that the price of the security is more likely to reach the strike price of the option.
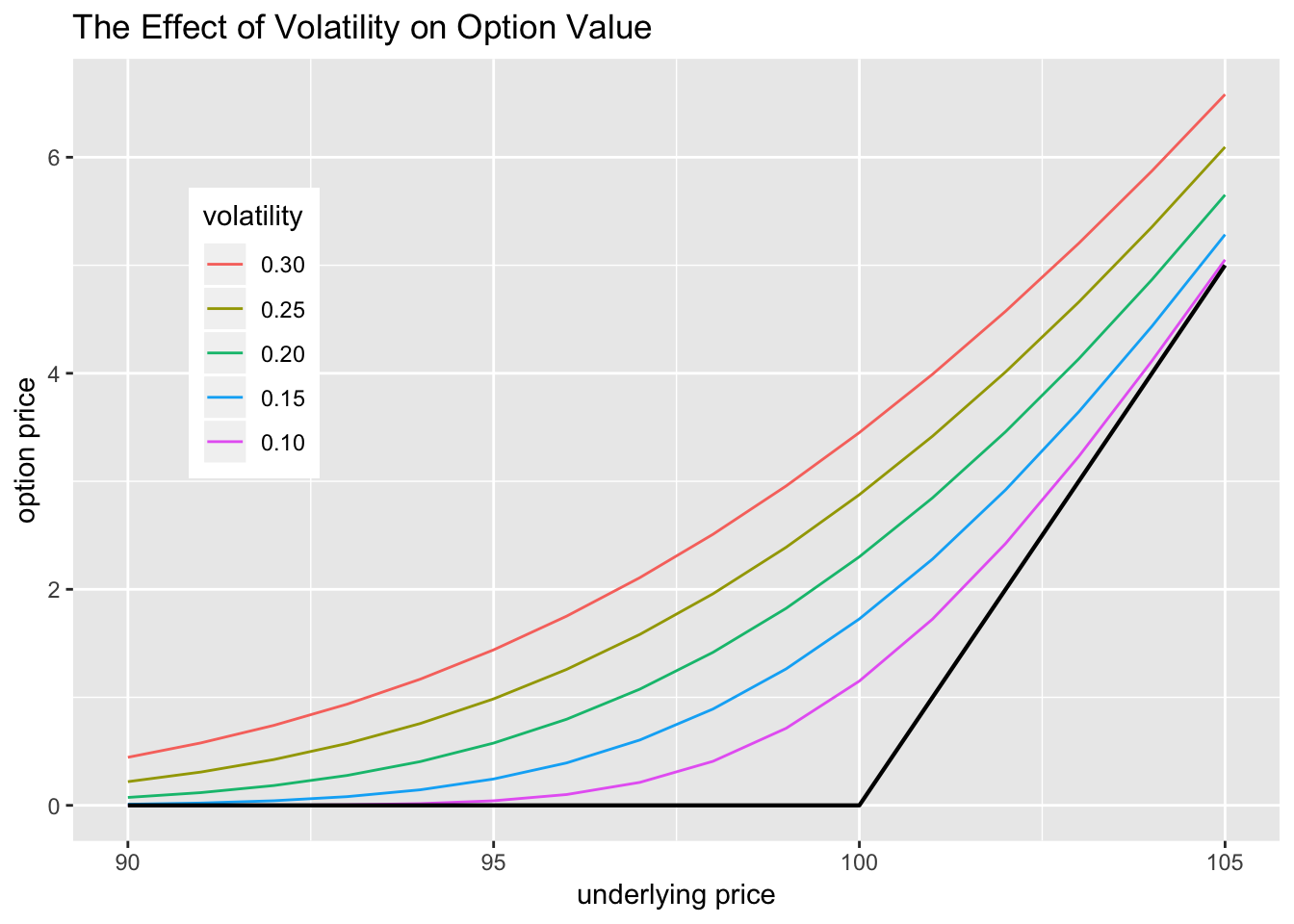
How the value of a call option changes with different levels of volatility
Source: https://pritamdalal.github.io/rff_book/option-pricing.html
In markets with asymmetric information, if all participants believe that some combination of goods will be sold, then that combination of goods is actually sold at equilibrium. In other words, at equilibrium, the expectations of market participants cause behaviors that result in the outcome being what the participants initially expected.
Assume there is a situation where traders A and B are both trading options on particular stock. In this example, A is the buyer and has more information than B about how likely it is that the price of the stock will become more volatile in the future. In this case, the transaction between A and B is very similar to the transaction taking place between an insurance company and an individual buying health insurance. The individual has more information about how likely the insurance contract will be to pay out in the future than the company does. In both cases, the buyers, A and the individual buying insurance, have a better idea of how likely it is that their insurance policy (option in A’s case) will increase in value in the future.
| A’s Value (Buyer) | B’s Cost (Seller) | |
| Low Volatility | 4 | 0 |
| High Volatility | 12 | 10 |
There are two possible situations for these traders, either the future volatility of the underlying security is low or high. Trader A has an idea of which is more likely in the future due to his superior information. If trader A believes volatility will be low in the future, then they will place a lower value on the option of a stock, however if they believe that volatility will be high in the future, then they will value the option more highly. If volatility is low in the future, then trader B has no cost since the option will not reach the strike price and they are unlikely to be assigned. If volatility is high, however, then trader B is obligated buy/sell a particular quantity of shares from/to trader A at the strike price. If the option is far in the money then this will be costly for trader B.
Since trader B has inferior data, they do not know if the price of the stock is likely to be more or less volatile in the future. They therefore determine the prices at which they will sell their option using their expectations. In the case where trader B assumes that there is a 50% chance volatility will be low and a 50% chance volatility will be high, the expected cost for trader B is (0.5)*0 + (0.5*10)=5>4. Under this assumption, trader B will be willing to sell the option at 5. This is however, greater than the price of 4, which is what trader A is willing to pay if they believe that volatility will be low in the future, meaning that trader A will only buy the option from trader B if A expects volatility to be high in the future. This is therefore not an equilibrium, because B’s assumption was that there was a 50/50 chance of the transaction taking place when there was high/low volatility, but A will only buy the option if there is high future volatility. The expectation does not cause itself to come true.
Another case, is if B assumes that future volatility will be low. In this case, these options are only worth 4 to A, and at a price of 4, A will be willing to buy the options whether they expect the volatility to be high or low. Once more, B’s expectation does not fulfill itself.
If B expects that volatility will be high in the future, then their expected cost is 10. This is less than A’s value for the option in a world with high volatility, so the option will be sold for a price between 10 and 12. Therefore, this situation represents an equilibrium.
In conclusion, while it is worth noting that option prices are determined by factors other than volatility of the underlying security (interest rates, time to expiration), using asymmetric information equilibrium, it is possible to see how activity in options markets can be used to gauge traders’ expectations. If options on a stock are highly priced, then this means that it is expected that other traders will buy when volatility is high, and in fact, this expectation fulfills itself. This is a phenomenon commonly observed before earnings announcements. The expectation of high volatility leads investors to price options so that they will be bought during periods of high volatility, but not during low volatility.
