Page Rank Through Linear Algebra
The concept of page rank and the algorithmic process where search engines rank pages have sparked my interest. Recently in other classes I am concurrently taking, we have taken a look at a concept similar to Page Rank from a different mathematical perspective. The article “Introduction to Markov Chains” by data scientist Joseph Rocca describes this process in depth which I will use to further explore this topic by adding more of a quantitative perspective to what we discussed in class.
The article begins by diving into Markov Chains which can be used to model certain mathematical patterns that appear in data collection and networks. A Markov chain is a sequence of probabilities that model the “next outcome” in a series based solely on the “current outcome” of the system.
Ex) Let a Markov Chain be defined by the set Z = {X0, X1, X2, …., XN} where each X is a probability outcome in the ordered sequence. The probability sequence starts at X0 and after a transformation becomes X1. Now the same transformation is applied on X1 which results in X2. This transformation can continually be applied until an equilibrium is reached.
Next, Rocca describes how Markov Chains can model a user moving from page to page on the internet which extends to the real-life application of billions of users navigating the internet. These chains are important because they can be used to rank the order pages appear on search engines in terms of importance where importance is defined by the number of users visiting a page.
Each probability outcome X is really a fair probability vector whose components correspond to the probability that a user moves to that node.
Ex)
Probability vector for A = [ 0, ½, ½ ] where there is a 0 probability material goes to itself, and ½ probability material goes to B or C
These probability vectors can be combined to create a square matrix where each probability vector is a column of the matrix. This matrix is the key to outputting new elements in a Markov Chain. This is because
Eventually as the matrix A or transformation is applied to Xc over and over again there reaches an equilibrium point where a steady state is achieved. This steady state is the expected outcome of users navigating through pages that are linked.
Mathematically this can be shown where:
X is the steady state/ equilibrium and is contained in the null space of B where Null(B) is the solution to XB=0. Now let’s look at a model of a network:
| A Out | B Out | C Out | D Out | E Out | F Out | G Out | H Out | |
| A | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| B | 1/2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C | 1/2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| D | 0 | 1/2 | 0 | 0 | 0 | 0 | 0 | 0 |
| E | 0 | 1/2 | 1/2 | 0 | 0 | 0 | 0 | 0 |
| F | 0 | 0 | 1/2 | 0 | 0 | 0 | 0 | 0 |
| G | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| H | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
The table above represents the probability of a fair user transferring from page to page. For example, from node A there is a 0.5 probability to go to node B and node C and a 0 probability to any other node.
There are many methods to obtain a solution to the linear equation BX=0. One method is row reducing matrix B augmented by the O vector. For brevity the steps of this calculation will be skipped.
Null(B) can be found by identifying the column Y of the nxn matrix with free variables and multiplying every entry by -1 and replacing the Yth entry of the column with a 1. In this case the free variable column is 8 and so every entry is multiplied by -1 and then the 8th entry is made a 1.
Finally, each entry of the matrix solution is multiplied by 1/ (sum of all entries) in order to “normalize” the solution.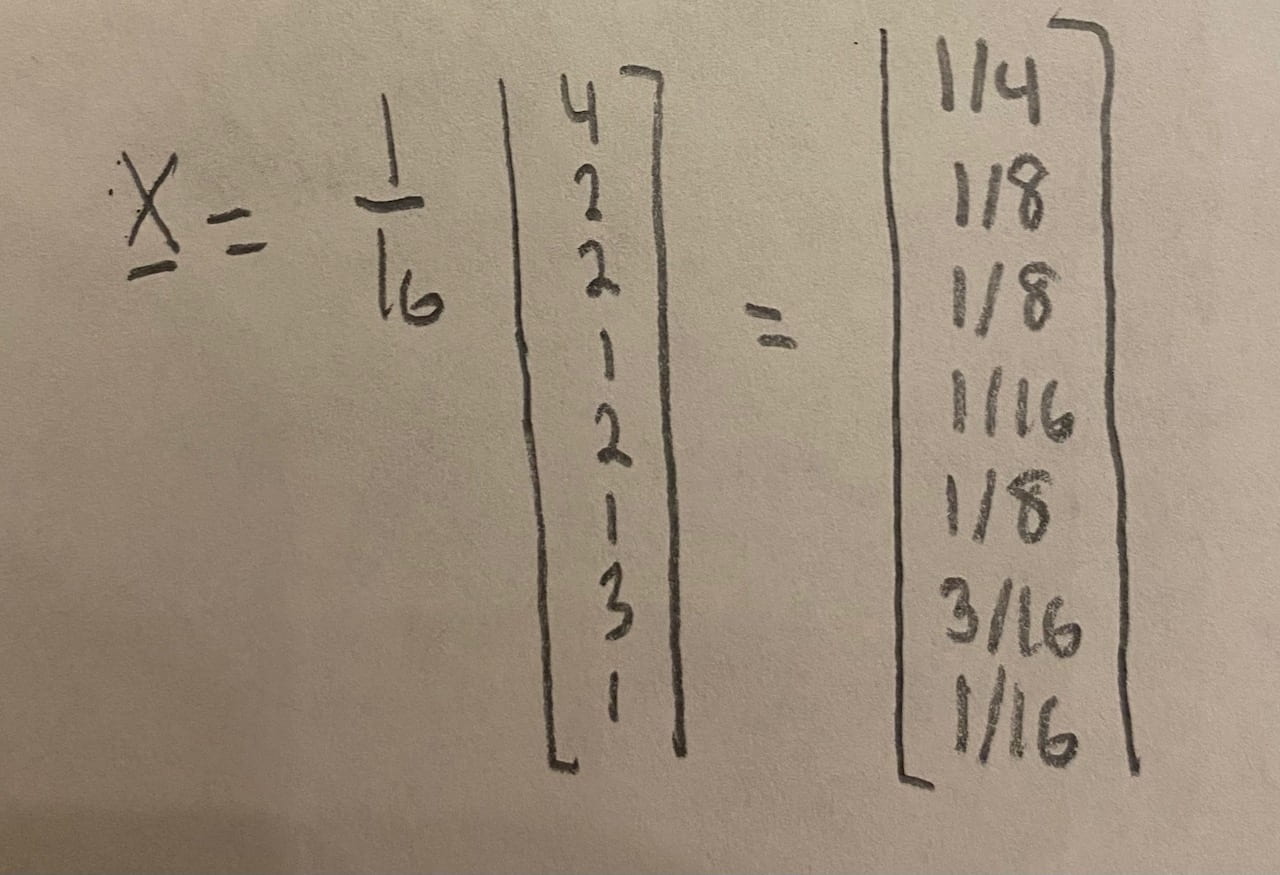
This solution explains that A=1/4, B=1/8 C=1/8, D=1/16, E=1/8, F=1/16, G=3/16, H=1/16
This method obtains the same solution as the method performed in class. The method discussed in class is faster than this linear algebra approach to this problem, but as the model you look at scales to the size of the internet it is no longer practical to compute by hand and using linear algebra fixes this. I found the mathematics behind the Page Rank algorithm extremely fascinating and even though the current google algorithm is part secret and has improved significantly from this model, it is interesting seeing the model that revolutionized the internet and how people navigate across it.
Sources:
https://towardsdatascience.com/brief-introduction-to-markov-chains-2c8cab9c98ab
Lay, David C., et al. Linear Algebra and Its Applications. Pearson, 2020.









