Game Theory, Embeddedness, and The Spread of Coronavirus
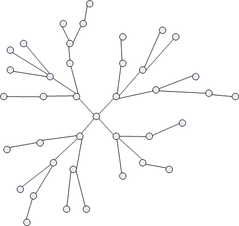
Wikipedia cites the “80-20 rule” as that for many events, 80% of the effects come from 20% of the causes. In a network, the use of local bridges connects different groups of people that mainly interact with one another. This principle of the 80/20 rule applies perfectly to the outbreaks of the COVID-19 pandemic as well. A recent study done in Hong Kong through contact tracing found that on average, 80% of cases involving contact tracing methods proved 20% of individuals were responsible. When we look at the interconnectedness of most networks, there are a few nodes (individuals) that connect certain groups of people. The nodes that contain many weak ties are likely the people that have the least amount of numerator embeddedness but tend to have the most denominator embeddedness. This means that the connections of both the node with many weak links and the one into a subgroup share few connections (numerator embeddedness), but they almost certainly connect to a number of nodes individually (denominator embeddedness). The figure below shows that the central node shares no two connections with each of the four components, but has denominator embeddedness of 16. This essentially means that these interconnected nodes are much more connected to many individuals and poses a serious problem with the emergence of COVID-19
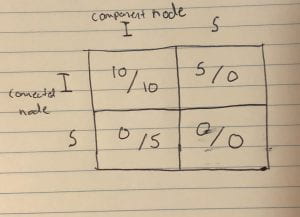
The connectedness of these individuals means that they are involved in many different groups of people. It makes sense then that these people would be conducive to the 80/20 rule of spreading COVID-19, but does not necessarily answer the main problem — how the virus is spread. In order to answer this question, we need to look at the decisions that these interconnected individuals make. Game theory allows us to explore this more in-depth. Individuals like our central node are given a number of different possibilities in the world of social interaction. The main way the virus is spread is through social interaction — that is going out to parties, involving themselves in the groups that they are associated with, and being the socialites that analytically they are. Given the decision to make these decisions, they are posed with the problem of whether or not to interact with the groups they are involved in. For this example, the decision to be involved by our component node and our connected node gives them each +10 satisfaction. If the interconnected node gets involved, but the component node stays in, this gives the component node +0 satisfaction and the connected node +5 satisfaction. The Nash equilibrium in this case is that both nodes get involved in social interaction, meaning there is a higher risk of the spread of COVID-19. Because of the nature of our connected node being involved in many groups, they have a high probability of being a carrier of COVID-19 and thus a more volatile spreader of the virus. The 80/20 rule is thus proved in this case because of the connected nodes higher probability of choosing to go out as well as their interconnectedness with different components in the network.
Source:
https://stateofreform.com/covid-19/2020/05/how-the-80-20-rule-may-apply-to-covid-infection-and-transmission/