The Dark Knight: Game Theory
The Dark Knight is the second installation of The Dark Knight Trilogy directed by Christopher Nolan. The film was widely acclaimed by many critics and considered one of the most popular superhero movies of all time. The premise of the movie involves a lunatic-like villain, the Joker, whose goal is to plunge the city into anarchy. Batman, along with the police and the District Attorney, attempts to arrest him. Throughout this movie there are various examples of game theory in action.
https://www.youtube.com/watch?v=vLastTrOkMw
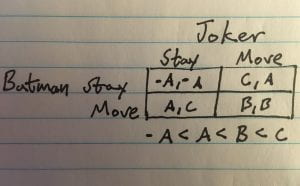
The first major example occurs in the middle of the movie. The Batman plays a game of chicken with the Joker. Batman on his bike rides towards a crashed armored truck at full speed. The Joker suddenly appears and stands in his path. If Batman hits and kills the Joker, he would have eliminated his nemesis but also would have destroyed his image as an altruistic savior. The Joker’s goal was to destroy Batman’s image and prove to the city that Batman isn’t what they think he is. But he also does not want to die. Both of them aim to get the other person to “chicken out”. We can create a 2 by 2 game theory matrix where we have payoffs -A, A, B, C. If they both refuse to move, both of them lose something precious to them. If they both move, the fight continues. If one of them moves while the other doesn’t, the one that stays gets the upper hand. The values of the payoffs are as follows -A < A < B < C. There are no dominant strategies or Nash Equilibriums.
In the movie, Batman chickens out while the Joker stays in place. The Batman crashes while the Joker gets the upper-hand in the fight. However, Batman protects his image. The payoff in this case would be A for Batman and C for Joker. C > A but also A > -A.
https://www.youtube.com/watch?v=K4GAQtGtd_0
A more famous example is the final scene of the movie. There are two ferries crossing the river. One contains ordinary people, families, children. The other contains prisoners, police, and military personnel. Both ferries are laden with explosives. Each boat also has a remote that if pressed would lead to the detonation of the other ferry. One of the ferries must be blown up by the other by 12:00 am or the Joker will blow up both of them. This creates a game that resembles the prisoner’s dilemma. Both boats have a weakly dominated strategy to press the button. There is a Nash Equilibrium where both ferries will choose to press the button. This would have the worst possible outcome for both boats.
Thankfully, both ferries do not choose to use the remote and Batman disarms the Joker resulting in both boats surviving. However, had Batman not been there the Joker would have blown up both boats. While this is not a perfect example of the prisoner’s dilemma, it comes very close.
Sources:
https://www.denofgeek.com/movies/the-dark-knight-the-joker-and-game-theory/