Using game theory to help a squash player improve their game
Squash is a high-speed, intense racket sport played by two players in a four-walled court. The game involves players taking turns to hit a small, hollow rubber ball onto the front wall, while one can use the other three walls as well. The primary objective is to play the ball in a manner that makes it difficult for the opponent to make a valid return, thereby scoring points. It is the only racket sport that is not played across a net.
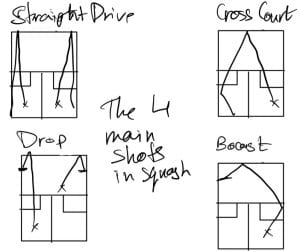
Squash involves a variety of shots, each with its strategic importance:
- A straight drive A basic shot hit straight down the wall to the back of the court. It is mainly used for defense, but it can also make the opponent give you a weak shot/ lose the point if its too deep down the length of the court.
- Cross Court: A shot hit from one side of the court to the other, traveling diagonally across the middle. It’s used to move the opponent across the court. Same purpose as straight drive.
- Drop: A delicate, soft shot aimed just above the tin (like what the net is in tennis), landing close to the front wall, primarily used to catch the opponent off guard, move them to the front of the court, which is tough to pick up and can make one win the point.
- Boast: A shot using the dimensions of the court where the ball is hit against one of the side walls before it reaches the front wall, used for both defensive and attacking plays.
Game Theory and Payoff Matrix
Game theory, in the context of sports like squash, involves strategic decision-making where each player anticipates and responds to the strategies of their opponent. A key concept in game theory is the payoff matrix, a table that shows the payoffs for each player for every possible combination of strategies. It helps in visualizing the outcomes of different strategies and in making strategic decisions.
Analysis of a Squash Game
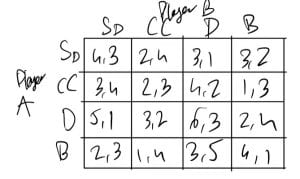
To analyze the squash match between Player A and Player B, where Player A wins 3-2 with the scores 11-7, 8-11, 11-8, 11-13, 11-9, we can create a 4×4 payoff matrix. This matrix will represent each player’s success with different shots: Straight Drive (D), Cross Court (C), Drop (Dp), and Boast (B). The values in the matrix will reflect the number of points each player won with these shots.
To analyze the squash match between Player A and Player B, where Player A wins 3-2 in a best of 5 match with the scores 11-7, 8-11, 11-8, 11-13, 11-9, we can create a 4×4 payoff matrix. This matrix will represent each player’s success with different shots: Straight Drive (D), Cross Court (C), Drop (Dp), and Boast (B). The values in the matrix will reflect the number of points each player won with these shots.
First, let’s calculate the total number of points played in all five games:
– Game 1: 11 (Player A) + 7 (Player B) = 18 points
– Game 2: 8 (Player A) + 11 (Player B) = 19 points
– Game 3: 11 (Player A) + 8 (Player B) = 19 points
– Game 4: 11 (Player A) + 13 (Player B) = 24 points
– Game 5: 11 (Player A) + 9 (Player B) = 20 points
– Total: 100 points
Now, let’s create the payoff matrix with the values from an analysis of the match. Each +1 is the number of points the player won on that shot in response to the other player’s shot.
In this matrix:
– The cell (SD,S D) indicates that when both players played Straight Drives, Player A won 4 points while Player B won 3 points.
– The cell (D, D) shows that when both players played Drops, Player A was more successful, winning 6 points compared to Player B’s 3 points.
– eg interpreting (SD, D) in instances where Player A hit a Straight Drive (SD) and Player B hit a Drop (D), the outcome was that Player A won the point 3 times, and Player B won it once. It shows that player
This interpretation of the matrix helps in understanding how each player’s choice of shot impacted the game’s outcome in specific situations. It indicates that in this particular match-up (Straight Drive by Player A vs. Drop by Player B), Player A had a strategic advantage.
This matrix provides a framework for analyzing the effectiveness of different shots and strategies employed by each player during the match. By studying the payoffs in various scenarios, coaches and players can gain insights into which shots were most effective and how the players might adapt their strategies in future games.
This analysis demonstrates the strategic variety in squash and how players’ choices of shots impact their game performance. The use of game theory and payoff matrices provides valuable insights into the decision-making process in competitive sports like squash, helping players and coaches devise more effective strategies for winning. This can be integrated into the training schedule of players.
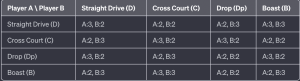
- For each of Player A’s strategies, we look for the best response by Player B.
- When Player A plays a Straight Drive, Player B’s best response is a Cross Court (A:2, B:4).
- When Player A plays a Cross Court, Player B’s best response is a Straight Drive (A:3, B:4).
- When Player A plays a Drop, Player B’s best response is a Boast (A:2, B:4).
- When Player A plays a Boast, Player B’s best response is a Drop (A:3, B:5).
- Conversely, for each of Player B’s strategies, we find Player A’s best response.
- When Player B plays a Straight Drive, Player A’s best response is a Drop (A:5, B:1).
- When Player B plays a Cross Court, Player A’s best response is a Drop (A:3, B:2).
- When Player B plays a Drop, Player A’s best response is also a Drop (A:6, B:3).
- When Player B plays a Boast, Player A’s best response is a Straight Drive (A:3, B:2).
Looking at these responses, it seems there is no pure strategy Nash Equilibrium in this matrix. In a Nash Equilibrium, both players’ strategies would be best responses to each other, but this doesn’t occur in any of the shot combinations here.
Interpretation for Players A and B:
- The absence of a pure strategy Nash Equilibrium suggests that there is no single combination of shots where both players would find no benefit in unilaterally changing their strategy.
- This indicates a dynamic and unpredictable nature of the game, where players need to continuously adapt their strategies based on the ongoing play.
- It suggests that both players might need to consider mixed strategies (a combination of different shots) rather than relying on a single type of shot throughout the game.
- The matrix highlights the strengths and weaknesses of each player against specific shots, offering insights into potential areas of improvement and strategy development for future games.
Finding any strategy being strictly dominated means that shot leads to lower payoffs in every situation To determine if any strategy is strictly dominated in the given matrix, we need to compare each strategy’s payoffs to see if one strategy consistently results in a worse outcome than another, regardless of the opponent’s actions.
Analyzing Player A’s strategies:
– Straight Drive (SD) vs. Cross Court (CC): D yields more points against Player B’s D and C, but less against Dp and B.
– Straight Drive (SD) vs. Drop (D): Dp yields more points against all of Player B’s strategies.
– Straight Drive (SD) vs. Boast (B): B yields more points against Player B’s C and Dp but less against D and B.
– Cross Court (CC) vs. Drop (D): Dp yields more points against all of Player B’s strategies.
– Cross Court (CC) vs. Boast (B): No consistent superiority.
– Drop (D) vs. Boast (B): Dp yields more points against Player B’s D and C, but less against Dp and B.
From Player A’s perspective, the Drop (Dp) strategy strictly dominates both the Straight Drive (D) and Cross Court (C) strategies. This makes sense because the drop shot is one of the toughest shots to pick up.
Analyzing Player B’s strategies:
– Straight Drive (SD) vs. Cross Court (CC): D yields more points against Player A’s D and C, but less against Dp and B.
– Straight Drive (SD) vs. Drop (Dp): Dp yields more points against Player A’s D and B, but less against C and Dp.
– Straight Drive (SD) vs. Boast (B): No consistent superiority.
– Cross Court (CC) vs. Drop (D): Dp yields more points against Player A’s D, but less against C, Dp, and B.
– Cross Court (C) vs. Boast (B): B yields more points against Player A’s Dp and B, but less against D and C.
– Drop (D) vs. Boast (B): No consistent superiority.
From Player B’s perspective, no strategy is strictly dominated by another.
Conclusion:
– For Player A, the Drop (Dp) strategy strictly dominates both the Straight Drive (D) and Cross Court (C) strategies.
– For Player B, there is no strategy that is strictly dominated by another.
This analysis suggests that Player A might consider focusing more on the Drop shot, given its overall effectiveness compared to other strategies. However, Player B does not have a clear strategy that is consistently outperformed by another, indicating a more balanced range of effective shots.
Lets consider a different match with these payoffs:
In this adjusted matrix, no single strategy strictly dominates another for either player, and there’s no clear pure strategy Nash equilibrium. This setup suggests that a mixed strategy Nash equilibrium might exist.
What a Mixed Strategy Nash Equilibrium Means in this Context:
A mixed strategy Nash equilibrium in the context of squash implies that players will randomize their shot selection, choosing different shots according to specific probabilities that make their opponent indifferent to their own shot choices. In other words, each player mixes their strategies (shot types) in a way that their expected payoff is maximized given the mixed strategy of the opponent.
For Player A and Player B, this means:
- Neither player will settle on a single type of shot as their constant strategy.
- They will vary their shots, keeping their opponent guessing and unable to predict the next move reliably.
- The probabilities with which they choose each shot type are calculated so that changing their strategy wouldn’t give them a higher expected payoff, given the strategy of the other player.
In practical terms, this reflects a highly dynamic and unpredictable game where players continually adapt their strategies, and the game doesn’t settle into a predictable pattern. The mixed strategy equilibrium represents the players’ optimal response to the uncertainty and complexity inherent in their opponent’s shot selection.