Game Theory of Stacking in Lineups
Hamilton & Romano: Equilibrium Assignments in Pairwise Team Contest
Presh Talwalkar: The Game Theory of Stacking Matchups in Your Favor
I play on Cornell’s squash team and our 2019-2020 season just began. This had me thinking about the lineup decisions our coach will be tasked with within the coming months. This decision can be described mathematically as a two-player game between Team A and B. In a given match, each coach must choose a lineup consisting of the order in which $n$ players will play. Each lineup represents a single strategy a coach can “play.” With $n$ players, there are $n!$ strategies available to each coach. Given the two strategies, we can examine each of the $n$ matchups. For every possible pair of players with one player from Team A and one from Team B, we assume we know which player will win should they play. Hence, the payoff for each team for a given pair of strategies is equivalent to the number of matches each team wins respectively.
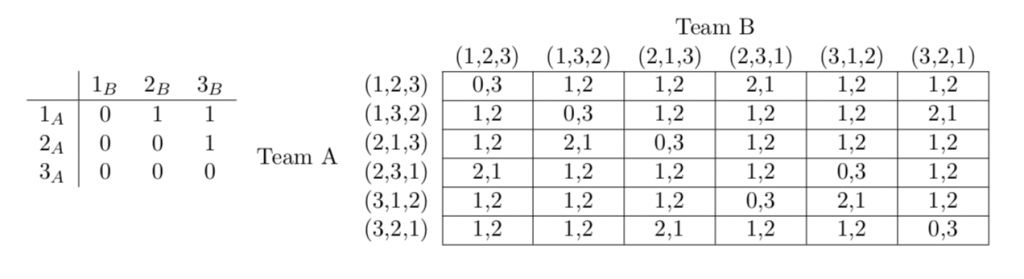
Let us consider the following small example:
Each team must choose an ordering of 3 players hence each coach has 6 strategies to choose from. We represent each lineup as a sequence (x1,x2,x3) where player x1 plays the first position and so on. In this example, lineup (1,2,3) represents the true ordering of the players. The matrix on the left has value 0 if Team B wins the match-up and 1 if Team A wins the match-up. Furthermore, the payoff matrix is shown on the right. We can see that Team B wins 3-0 in 4/6 of the strategy pairs, wins 2-1 in 1/6 of the pairs, and loses 1-2 in 1/6 of the pairs. If we assume that Team A knows Team B’s lineup, they can always choose the unique strategy resulting in their victory. However, coaches must make lineup decisions simultaneously and independently.
Ideally, coaches should choose their lineup in accordance with the actual ranking of their players. Deviating from this ideal lineup to gain a competitive advantage is a phenomenon known as “stacking.” I wondered: if both teams stack, what happens? What is the Nash-Equilibrium? Fortunately, I found the answer to this question in the linked articles. The Hamilton and Romano paper describes a more general model than the one I present in this post. They show that both coaches stacking results in a mixed-strategy equilibrium in which every strategy is played with equal probability. Hence, the lineups become completely random. Herein lies the reason why stacking is not allowed in competition.
Let us revisit the example game. If both teams play their true lineup, Team A always loses. However, if Team A chooses to stack (and Team B does not), they will always win. If Team B chooses to stack (and Team A does not), they will play their true lineup and always win. Lastly, if both teams stack, they have no information on which to base their decision. Hence, they play each strategy randomly and Team A has 1/6 of winning and Team B has a 5/6 chance. In fact, we have created a new game in which Team A has a dominant strategy of stacking. Team B’s best response is to stack as well and both teams stacking becomes a pure Nash-Equilibrium.
Other thoughts and questions
Because stacking is regulated in competition, a coach who chooses to stack must avoid stacking so severely that they are detected. For example, the stacking required for Team A to win (given Team B plays their true lineup) is as severe as it gets. Their worst player is playing their top position. Consider some measure of stacking severity and eliminate strategies that are more severe than some threshold. What happens to the Nash-Equilibrium of the resulting game?
How do we define the better team in this scenario? What if using true lineups yields a winning team that only wins a minority of possible pairs of strategies? Is this even possible?
Feel free to reach out to me if you tackle any of these questions! I’d love to know what you think!