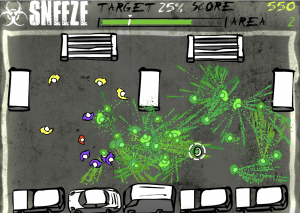
Sneeze
https://www.miniclip.com/games/sneeze/en/
When I was ten or so, I became obsessed with simple online strategy games, neglecting doing my homework on my first laptop in order to play them. In the Miniclip.com game Sneeze, you have one sneeze to infect a target percentage of the population. The people around you move in random patterns and fall into three categories – child, adult, or elderly. Older people move for longer before sneezing but they move slower. Younger people move faster and have sneezes that affect a broader area but have a lower probability of being infected, even if they are within a sneeze infection area. Levels get progressively harder by increasing the goal affected population percentage and changing the proportions of each age group. While the first few levels seemed simple, my sixth grade self could never pass all ten levels, getting stuck around level 7 – 70% infection.
This game is a visual, interactive example of the Branching Process of epidemic spreading discussed in class. There are far more variables added: the motion rate, the motion pattern, the incubation time, the sneeze radius, and the infection likelihood for each group, along with the number of people from each group and their starting positions. However, at its most basic, Sneeze follows the Galton-Watson process. This process has two parameters – the number of contact and the probability of transmission. Here, the number of contacts (k) is governed by the sneeze distance and the random number of people that happen to be moving through the affected area. The probability of transmission (p) differs between age groups but carries a distinct value for each. Also importantly, there is no overlap between infection waves – as soon as a character has sneezed, they stop moving and cannot become re-infected. The specific basic reproductive number is beyond what I could calculate without knowing the code for the program, but since p and k are both well defined, it could hypothetically be calculated and used for further analysis of the contagion process.
Sneeze is a computer game, and with its constant variations in population makeup and individual motion, I recognize that I stood no chance of ever winning at age 10. However, with my new knowledge of the Branching Process and generally more sophisticated reasoning ability associated with my age, I don’t see it as quite so daunting.
https://www.miniclip.com/games/sneeze/en/