Game Theory On a British Game Show
https://www.youtube.com/watch?v=zpahL4fu5R8
This video clip is from a British game show called Golden Balls. Two players, Steve and Sarah, play in the game, where each of them have two choices–split or steal the 100,000 British pounds. If both of them choose split, they will each get 50,000 pounds. If one of them chooses split and one chooses steal, the person who chooses steal will take all the money home while the other one gets none; and if both of them choose steal, then none of them get the money. In the video, both of them tried to convince each other that they will choose split. However, in the end, Sarah chose steal and Steve chose split, which means that Sarah won all the money.
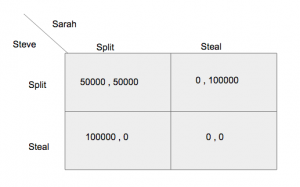
If we draw a payoff matrix for this game,
we can see that Steve and Sarah have a dominant strategy of playing steal. But this will get them both ended up with zero. But winning 100,000 pounds is very tempting that we can expect someone will choose to steal.
This is very similar to what we talked about in class about prisoner’s dilemma, where prisoners are given choices of denial or confession. The dominant strategy is confession and prisoners often ended up both confessing, which leads them to the worst outcome of the game. And the concept of Nash Equilibrium also plays a role in the game. Because the best response for each player was to steal, the Nash Equilibrium was steal steal.
However, there is a slightly difference between the two, because in Golden Balls, the two players can talk to each other, while in the prisoner’s dilemma, prisoner’s can not communicate. The quick conversation between Steve and Sarah led to Sarah’s betrayal because she can now assume Steve will actually play split for their own benefits. It was smart for Sarah to play her dominant strategy, but the audiences would hate her now.