Mixed Nash Equilibrium as applied to Match Racing in Sailing
On a fundamental level, match racing, more than any other genre of sailing, is based on the idea of anticipating your opponent. Match racing involves only two boats that race solely each other; This causes the tactics involved to be much different than in a “fleet race,” where each individual boat has many other opponents and is racing against all of them at once. The most important part of a match race is the “pre-start.” During this, each of the two boats jockey for a better position against her opponent. Whichever boat can use the racing rules of sailing more effectively, has a better chance of remaining in front of the other for the rest of the race. I.e. sailing is a sport where the rich get richer, so starting out with an advantage, even if it’s a small one, is very important. Particularly in match racing, being inches ahead off the starting line often is the difference between winner and loser. For more information on the logistics of match racing, please see the following link: http://www.boat-duesseldorf.com/cipp/md_boot/custom/pub/content,oid,11712/lang,2/ticket,g_u_e_s_t/local_lang,2
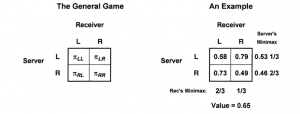
In their Minimax Play at Wimbledon (http://www.calpoly.edu/~aamendes/GTweb/tennis.pdf), Walker and Wooders gather information about professional tennis players’ serves. These players are presumed to have a decent sense for each other’s tendencies to server to the left or right side of the service box. Walker and Wooders constructed models using the likelihood that the server would win a point by serving to a particular side, versus the likelihood that the receiver would “overplay” a particular side. In doing so, they were able to create 2×2 point-game models by analyzing the data and finding a strong correlation between the mixed Nash equilibrium for where a server should serve and where the server actually served. Thus, the players would “randomly anticipate” their opponents, which lead to a mutually maximized payoff for both players.
In much the same way, gaining an advantage over your competitor at the beginning of a match race involves anticipating which maneuver she will try in order to gain control over you and prevent her from losing control to you. It is important to note that match racing is often done in large boats that tend to have a lot of momentum, do not respond quickly, and take a considerable amount of time to complete a maneuver. For simplification purposes, consider a situation where the two boats are sailing towards each other and the boat on the right has the right-of-way over the boat on the left. The boat on the left must avoid the boat on the right and can either try to go down below the right boat or up above the right boat. The right boat wants to choose the same direction as the other boat in order to gain control over them, since she has right of way. If both choose down in the situation, the right boat will have gained a more significant amount than if both boats choose up. With this information, lets construct the following purely hypothetical 2X2 point game model for this situation with the left row representing the left boats choice and the top row representing the right boats choice; note that the number in each cell represents the probability of the right boat winning the race:
| UP | DOWN | |
| UP | .65 | .45 |
| DOWN | .55 | .75 |
There is no pure Nash Equilibrium in this table, so some mixed Nash equilibrium must exist. Although this is a simple example, there are a lot of ways two big match race boats could cross paths that would lead to a relatable scenario with no Nash Equilibrium, and I hypothesize that professional match racers, who are familiar with their opponents, follow said Nash Equilibria to a significantly close extent. Its kind of fun to structure intuitive sports psychology that I have personal experience with using Game Theory.