Gaming the System: A Prisoner’s Dilemma in the Game Show “Golden Balls”
Source: http://www.radiolab.org/story/golden-rule/
This segment of a RadioLab episode is about the ending of a British Game Show, Golden Balls. The main part of the show is about people adding money in various ways to the jackpot, but the very last segment of the game is a sort of Prisoner’s Dilemma among two finalists: they can each choose to “Split” or “Steal” the money. If they both Split the jackpot, they each get half the money; if they both Steal the jackpot, they each get nothing. If one Steals and the other Splits, the stealer takes all the money and the splitter receives no money.
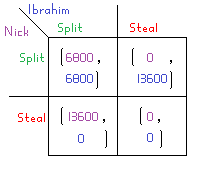
This RadioLab episode is about one specific instance that played out particularly oddly. The players are named Nick and Ibrahim, and the jackpot is £13600. The payoff matrix is therefore as follows:
At first glance, this payoff matrix is extremely similar to that of the Prisoner’s Dilemma, with “Split” equating to “Don’t Confess” and “Steal” equating to “Confess.” However, there is one key difference: instead of doing strictly worse if you Split and your opponent Steals than if you both Steal, the payoffs in both cases is identical. There are therefore three Nash Equilibria: everything except (Split, Split).
However, RadioLab notes that there is another factor: there is a social stigma of feeling like a “sucker” when you are stolen from. This “sucker stigma” does in fact make being stolen from worse than both trying to steal. Arbitrarily, I assign this stigma a value of -10 for this; the exact number doesn’t matter, as the analysis of the game remains the same as long as this number is less than zero. This change makes the game become analytically the same as a Prisoner’s Dilemma: the Nash Equilibrium and therefore the expected outcome is (Steal, Steal).
The other major difference here is that, unlike in the Prisoner’s Dilemma, the people are allowed to communicate with each other. This change does not directly affect the payoff matrix, but is one of the key differences, since this change allows people to change each others’ payoffs and strategies by making promises.
In particular, Nick makes a very odd claim: he tells Ibrahim straight-out that he will choose Steal, and Ibrahim cannot convince him to change his mind. Instead, Nick claims to share the money after the show. Assuming all of Nick’s claims are true, a row in the matrix is removed and one payoff in the remaining row is completely changed.
This payoff matrix leaves Ibrahim to choose between two choices, and clearly, the better option is to Split the money.
The validity of Nick’s promises may be extremely dubious, especially considering that he has very little incentive to go through with splitting the money after the show. However, due to the weirdness of this situation, the “sucker stigma” payoff is eliminated (it came from a social construct, and this situation is entirely out of the realm of social norms), so even if Nick lied, the game reverts to the original matrix, which is not a strict Prisoner’s Dilemma: if Ibrahim knows that Nick is going to Steal, he does not do better by choosing either strategy. Therefore, the entire possibility that Nick lied can effectively be ignored, as Ibrahim has no optimal strategy in this case.
Ibrahim therefore should ideally choose Split, given Nick’s promise to Steal the money and share it after the show.
So what ends up actually happening on the show? They both choose Split.
After all, once Nick has made sure that Ibrahim would choose Split, it does not matter in terms of payoff whether Nick Splits the money now or shares it later; Splitting it now would be a lot less of a hassle.
As a final thought: Ibrahim reveals to RadioLab that he would have, in fact, chosen to Steal, as would have been his optimal strategy in the “sucker stigma” matrix. So, as it turns out, communication and weird, counter-intuitive promises can, in fact, lead to outcomes that make everyone happy!