Collegetown Craze
The main topic of everyone’s conversations at Cornell the past few weeks has been housing for 2013. It is tradition at Cornell that juniors and seniors live in collegetown. And it is also tradition that you decide where you are going to live an entire year before you move into your apartment/ house. This rush puts a great deal of pressure on people to plan extremely far in advance. You have to know how much you can pay, where you are going to want to be, and whom you want to be with an entire year in advance. This leads to quick decisions that are not usually in your best interest that cause a great deal of regret. Personally, my friends changed a great deal last year and I would have chosen to live with different people if I waited to sign a lease until the spring. But, this would have left me in a less than ideal location. This article from the “Cornell Daily Sun” states that students should try to change this tradition by mutually agreeing to wait to sign leases until the spring semester. While this would be very ideal, it is very unlikely that this will happen. The article also talks about the problem of students’ willingness to pay a great deal of money for subpar living spaces causing landlords to charge an extremely high amount. These situations create both a prisoner’s dilemma and a matching problem.
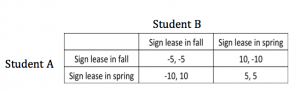
To analyze the prisoner’s dilemma in this situation, let’s take the two players to be two students at Cornell that want to live in collegetown the following year. Obviously there are more than two students that want to live in collegetown, but I picked two students, A and B, at random, so this argument can be expanded to any students at Cornell. Both students, A and B, each have two strategies that they can play, to sign their lease in the fall or in the spring of the year before they plan to live in collegetown. For example, this year students could choose to sign their lease in Fall ’12 or Spring ’13 for their living quarters for Fall ’13- Spring ’14. To assign the payoffs I am assuming that the students both want the same house to live in. This assumption allows me to model the situation with the prisoner’s dilemma. This is because if they wanted different houses it would not matter when the other student signed because they would not be competition with each other. If both students plan to sign their lease in the fall, their payouts will each be -5 (on a scale from -10, 10). This is because each student has a chance to get the house that they want, but they have to decide quickly what they want and whom they want to live with, so this outcome could cause some regrets. If one student signs their lease in the fall and the other in the spring, the student who signs earlier will have a high positive payoff, say 10 and the other student will have a really negative payoff, say -10. This is because the student who signs earlier will get the house they want and there is not as much pressure on them to sign within the first few weeks of school as long as they sign before the other student signs. This other student who waits until spring will not be able to get the house that they wanted because the other student already signed it. The last outcome occurs when both students wait until the spring to sign their leases. This leaves both students with a payoff of positive 5. This is because both students get to have a long time to think about whom they want to live with, where they want to live and how much they want to pay. Although there will be competition for which house the students get to sign, regrets are much less likely because the decisions were not rushed.
In this prisoner’s dilemma both students have the same dominant strategy, to sign in the fall. This is because given that the other student signs in the fall, this student has a higher payoff from signing in the fall (-5 versus -10). Given that the other student signs in the spring, this student benefits more if they sign in the fall (10 versus 5). Therefore the equilibrium will be that both students will play their dominant strategy and will sign in the fall. This outcome is proven to be true by the tradition that students at Cornell sign their leases very early in the fall semester. But, as this article states all of the students would be better off if we mutually agreed to wait until the spring to sign leases. By looking at the total social welfare of each outcome, we can prove this fact. With both students signing their leases in the fall the total social welfare in -10. Society is not better off because the students have to make quick uninformed decisions, which usually lead to regret. When one student signs in the fall and the other signs in the spring, the total social welfare is 0. One student is better off than the other but the society as a whole is no better off than before the housing craze. Lastly, the most socially optimal solution occurs when both students wait until the spring to sign their leases. This leaves society with a total social welfare of 10. Because both students can take their time to make educated housing decisions.
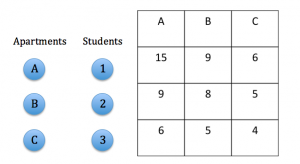
Another problem that this article addresses is the fact that the apartments and houses in collegetown are extremely over priced for what they are. This can be described by the matching problem. Lets take three apartments (A, B, C) in collegetown and three students (1, 2, 3) that want to live in collegetown. For this example lets assume that the apartments are one bedroom, so only one student can be assigned to one apartment. The first apartment (A) is very nice, close to campus, and relatively new. The third apartment (C) is very far away and very run down. And the second apartment (B) is somewhere in between the other two. Disclaimer, everything in collegetown is relative. Nothing is that nice; people just think some places are nice because they are not as bad as the rest. Below is a matching problem set up for this situation. I added arbitrary numbers for each person’s valuation of each apartment. Student 1 is willing to pay a great deal of money and student 3 is not. The valuations are in 100’s of dollars.
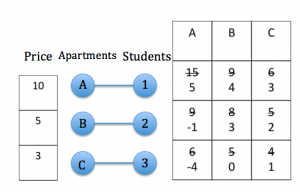
Now, lets look at the market prices of each of these apartments compared to what the students value them at. Realistically the prices of the apartments should be $600, $500, and $400 respectively. With these prices and the high willingness of Cornell students to pay a lot of money, all three students can buy all three apartments. Therefore the owners of the apartments realize that they can increase the price to a higher market-clearing price and still have renters each year. Here I am making the same assumption that the article makes: the owners want to make as much profit as they can. So in order to make the more profit, the relators raise their prices to $1000, $500, and $300 respectively. With these new prices, each student’s updated valuation, price for each person, becomes his or her old valuation minus the price of the apartment. These new valuations cause each student to want a different apartment the most, i.e. market clearing prices. This eliminates the competition and allows every student to get the house that they want. This can be seen in the following preferred seller graph.
This example with arbitrary numbers proves that when students are willing to pay a great deal for housing, the owners of the apartments will take advantage of the situation and raise their prices. Therefore, the article suggests that the students should not be willing to pay as much and the owners should not try to make as much profit. But, this is very unlikely to happen. Overall there is chaos in collegetown every fall semester. Students are trying to sign their leases as early as possible to make sure they get the “best” housing and the owners have very high prices because they know that college students will pay them.
Disclaimer: The values of the payoffs were assigned based on what I thought the payoff would be on a relative scale from -10, 10. These are not necessarily the exact payoffs. Also, the valuation and market prices in the matching problem are arbitrary to show an example.
http://cornellsun.com/node/48254
-MC