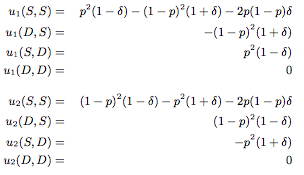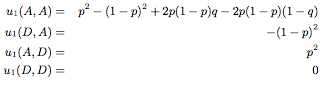Closer Look Into Cybersecurity via Game Theory
A blog about an academic paper that addresses cybersecurity by discovering the Nash Equilibrium in two game theory models.
Overview
As we progress in technology, cyber attacks have increased exponentially. Therefore, the United States community has been addressing issues involving cybersecurity risks to protect the nation’s information while asserting dominance in this new tech sector. My interest in cybersecurity has led me to discover research done in the academic paper, Cyber-sword v. cyber-shield: The Dynamics of US Cybersecurity Policy Priorities, which applies concepts that we learned in class.
This paper highlights the strategic decisions faced by states in dealing with software vulnerabilities. The two main strategic decisions involves either pursuing an offensive or a defensive action. Assuming that both players are using the same vulnerable software, an offensive action would be to use the discovery of a software vulnerability to harm the other side. A defensive action is the disclosure of the vulnerability, so that the software manufacturer can fix it. We will see through these models that at least one of the players will have an incentive to pursue an aggressive cyber action instead of defending and securing its own system. Because of this, cybersecurity policy makers are leaning to find ways to make both sides want to pursue the defensive option.
Applying Game Theory to Learn About the Environment Relating to Software Vulnerabilities
The academic paper discusses two game-theoretic models: vulnerability stockpiles and cyber hawk. These game theory models are similar to the ones we learned in class, in which there are players, payoffs and strategies. However, something new that is added are parameters such as p, q and delta.
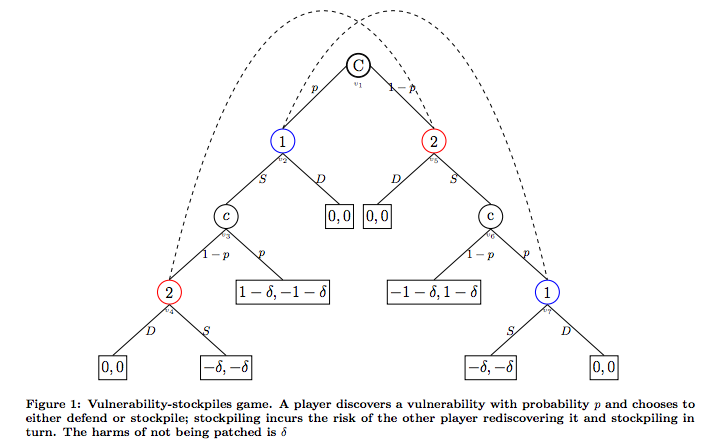
Game Theory Model 1: Vulnerability Stockpiles
The first model that we take a look at deals with two strategies, which are stockpiling (S = “stockpile”) and disclosing the vulnerabilities to improve security (D = “defend”). The article reduces the problem to two players (one is assumed to be the US) to predict the optimal behavior in response to each other’s cyber position. In the tree diagram, we see that both players, represented by 1 and 2, have the opportunity discover the software vulnerability.
Tree Diagram of the Vulnerability Stockpiles Game
On the left half of the tree diagram, we can see what happens when player 1 discovers a vulnerability. If player 1 chooses S (stockpile), then player 1 has an advantage of 1 – delta and the other player has the disadvantage of -1 – delta. However, if Player 2 discovers the vulnerability after Player 1, the playoff changes depending on Player 2’s strategy. If Player 2 chooses S (stockpile), the both sides lose out by the amount -delta. Since they both know that there is vulnerability, there is no longer an advantage to stockpiling. Instead, it would be better to disclose it so that it can be fixed. Note, that anytime player 1 or 2 chooses D (defend) as a strategy, the payoff is 0 for both players. This is true because defending has no strategic advantage or risk. The right hand side of the tree diagram demonstrates the same thing as the left half, but it applies to player 2.
Using the tree nodes, we can denote the payoff values for the different situations:
Expected Payoff for All Strategies For Both Players in the Vulnerability Stockpiles Game
Due to complexity of the calculations, I will not include it in this blog but refer to the link below for the reasoning behind the calculation.
The important concepts is that delta represents the amount of harm done to the general public if no one decides to defend their system. Overall, delta measures the social risk that occurs. Meanwhile, p represents the sophisticated level of a player’s technical experience, which means how well they will discover vulnerabilities.
The equilibrium is determined by the values of p and delta. The diagram below shows how the players can respond depending on each of their technical sophistication (p) and social risk (delta). We notice that when delta is 0, then both sides want to stockpile, which is the aggressive action in this model. Therefore, when no social cost or risk is involved, both sides will aggressively purse stockpiling. This is something we should keep in mind as we move to the next game model.
Nash Equilibriums for the Vulnerability Stockpiles Game
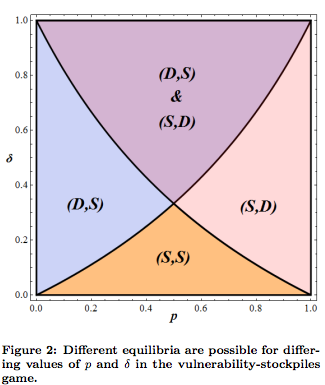
Game Theory Model 2: Cyber-Hawk Game
This game model is similar to the first model, but it considers the actual outcome of an attack. The first introduces the strategies stockpile and defend, which allows us to see the costs and benefits of being able to potentially exploit another. In this model, we will add the dimension of attack as a strategy in replace of stockpile. Therefore, the second model describes 2 strategies which are to attack or defend. Attacking means that a player discovers a software vulnerability and keeps it for exploit in the future. Let’s assume that the attack is successful, so the payoff is 1 and being attacked is -1. Defend means that the player discovers a software vulnerability and reveals it so that the issues are fixed. This means payoff is 0.
Tree Diagram of the Cyber Hawk Game
This tree diagram is similar to the concept of the previous tree diagram. The left hand sides deals with player 1 discovering the vulnerability first and the right hand side is when player 2 discovers the vulnerability first. Choosing D (defend) as a strategy will lead to payoff of 0. If player 1 attacks and player 2 doesn’t discover the vulnerability, then the payoffs are 1, -1, respectively. However, if player 2 discovers the vulnerability and attacks, the payoffs are depended on who attacks first. If player 1 attacks first, then it will lead to 1, -1, but if player 2 attacks first then it will lead to -1, 1.
Expected Payoffs for All Strategies for Both Players in the Cyber Hawk Game
Using the tree nodes, we can denote the payoff values for the different situations. Note: The payoffs are the same for the two players. Instead of delta, we have q which represents the aggression and likelihood a player will choose to attack after discovering a vulnerability. p is the same as before and represents the technical sophistication level of the players, which means how well they discover vulnerabilities.
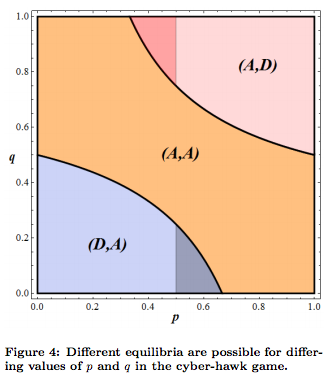
You can see from the diagram below that the equilibrium in this model is determined by the values of p and q. The diagram below shows how the players can respond depending on each of their technical sophistication (p) and likelihood of aggression (q). We notice that as the players have similar technical sophistication (p), then both will be more willing to attack (A,A).
Nash Equilibriums for the Cyber Hawk Game
In the first game model, if the social cost is not decided in the decision making process, both will play aggressively. The second game model, we notice that as the technical sophistication become similar for the players, they will be inclined to play aggressively. Overall, we noticed from both of the models that there is no equilibrium for the strategies (D,D). Therefore, both players are inclined to not take defense and the side that does will get the “short end of the stick”.
Conclusion
We can use these game theoretic models to explain observed behaviors and determine policy recommendations based on the predictions to create a more defensive equilibrium. The academic paper states that cybersecurity policy makers can promote defensive behavior through various methods. For example, we can increase the social cost (delta), maintain technical superiority (p) by ensuring they are consistent and different, and imposing transparency laws.
Overall, the main takeaway is that we can use the concepts from class to apply to situations such as cybersecurity to provide insight on observations. In this case, we observed how both players leaned towards an aggressive / offensive behavior, which is dangerous. Therefore, policy makers should intervene and consider ways to make players leaned towards a more defensive behavior.
Sources:
http://web.mit.edu/ecir/pdf/Friedman%20cyberwar-governance.pdf