Braess’ Paradox in Chemical Processes
Braess’ Paradox is the situation where a more convenient path between two points is added, yet the Nash Equilibrium payoffs for all the players are lower.
Sure, this sounds like a fun bit of trivia, but what if we got rid of human choice and replaced it with chemical equilibria? After all, chemicals have their own unique reaction pathways and rate of reactions. The article below demonstrates the processes required to examine Braess-like behavior in molecules:
http://link.springer.com/article/10.1007%2Fs10910-010-9746-7#page-1
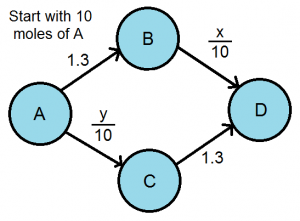
For the sake of explanation, we will examine a simplified version, which most likely does not exist. Consider a process that starts with 10 moles of A and you want to get as much D as possible.
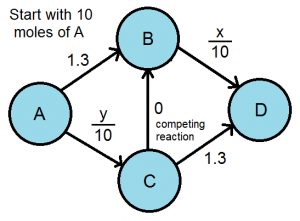
The nodes are all the chemicals that our process contains and the edges represent the time needed for reaction. There is also a molar dependence on the rate laws of the BD and AC reactions. We can determine the preferred reaction pathway by finding the Nash Equilibrium. In this case, x=y=5 moles. Given these options, the reaction pathway is very efficient. But what if we added another reaction, one that transforms C almost immediately into B?
We can already see the Braess’ Paradox from this diagram. The AC reaction is favored over the AB reaction because it has a faster rate. Similarly, the CBD reaction pathway is preferred over the CD pathway because it also has a faster rate, regardless of how many of the initial moles flow through. However, if all the molecules take the CB competing reaction, the time required to transform A to D is 2, which is actually longer than the time when there was no competing reaction. From this model, we can see that human behavior is not the only kind of decision making that can lead to unexpected results.
Of course, for any chemical process, there are many other variables at work which the article addresses and reconciles. Also, it deserves mentioning that for a competing reaction to represent Braess’ Paradox would probably require the use of a catalyst, to observe the difference between two pathways. Chemical processes may not be the best way to observe the effects of individual decision making, but they provide a model that compares outputs like payoffs, reactants like people, and unknown exterior variables like unknown exterior variables. Whether considering the social implications of a network, or finding the best way to make a chemical product, you need to do your research and model its behavior. You never know when Braess’ Paradox will mess up your new road, or your beaker that was sitting out overnight.